Частичная сумма ряда

[bayah]

Здравствуйте.
Вопрос такой - найти частичную сумму ряда:
$\sum\limits_{k=1}^\infty (\sqrt{k+2}-2\sqrt{k+1}+\sqrt{k})$

Если выписать первые члены последовательности:
$ \\ \sqrt{3} - 2\sqrt{2} + \sqrt{1} \\ \sqrt{4} - 2\sqrt{3} + \sqrt{2} \\ \sqrt{5} - 2\sqrt{4} + \sqrt{3} \\ \sqrt{6} - 2\sqrt{5} + \sqrt{4} \\ \sqrt{7} - 2\sqrt{6} + \sqrt{5} \\ ... $

Становится ясно, что сокращаются все диагонали из трех элементов, и в общем случае остается только $ - 2\sqrt{2} + \sqrt{1}$ из первой строки, $\sqrt{2}$ из второй, $\sqrt{k+1}$ из $k-1$ строки и $\sqrt{k+2} - 2\sqrt{k+1}$ из строки $k$.
Для случая $k>2$ можно еще сократить и останется только $- \sqrt{2} + \sqrt{1} + \sqrt{k+2} - \sqrt{k+1}$.
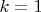
В случае $k = 1$ получится $\sqrt{3} - 2\sqrt{2} + \sqrt{1}$.

Вопрос: как это записать в одной формуле?
Вроде бы должно еще что-то сокращаться, но я тупой)
Придумал только так, типа кусочно линейная функция, где перелом в точки 2!
$ \\ S_k = \sqrt{1} - 2\sqrt{2} + (( ((n+2) - |n-2|)/2) - 1) \sqrt{2} - 2 \sqrt{n+1} + (( ((n+2) - |n-2|)/2) - 1) \sqrt{n+1} + \sqrt{n+2} $

[TOTAL]

bayah в сообщении #1159359 писал(а):

Для случая $k>2$ можно еще сократить и останется только $- \sqrt{2} + \sqrt{1} + \sqrt{k+2} - \sqrt{k+1}$.
В случае $k = 1$ получится $\sqrt{3} - 2\sqrt{2} + \sqrt{1}$.

Вопрос: как это записать в одной формуле?

$- \sqrt{2} + \sqrt{1} + \sqrt{k+2} - \sqrt{k+1}$ - это и есть одна формула

[bayah]

TOTAL в сообщении #1159362 писал(а):

$- \sqrt{2} + \sqrt{1} + \sqrt{k+2} - \sqrt{k+1}$ - это и есть одна формула

Фигасе! Точно! Я же говорил, что я тупой)