Составить линейную модель в задаче по статистике

[maked0n]

Доброго времени суток. Есть следующая задача:

Цитата:

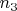
Взвешивание грузов массами $a$, $b$ и $c$ на одних и тех же весах производится следующим образом: $n_1$ раз взвешиваются первые два груза вместе, $n_2$ раз взвешиваются второй и третий груз вместе и $n_3$ раз взвешиваются вместе все грузы. В предположении, что все ошибки измерения имеют распределение $N(0, \sigma^2)$, построить доверительные интервалы уровня $1 - \alpha$ для всех четырех параметров.

Насколько я понимаю, я должен составить линейную модель, свести ее к гауссовской линейной модели, ну а дальше по алгоритму. Проблема у меня с составлением линейной модели: я не понимаю, как в одну формулу для $X_i$ "впихнуть" все массы так, чтобы получилось хорошо. Была идея сделать формулу какого-то такого вида: $X_i = p_1 \cdot a + p_2 \cdot b + p_3 \cdot c + \varepsilon_0 + ... + \varepsilon_i$, где $p_1, p_2, p_3$ - какие-то параметры, которые должны как-то зависеть от $i$ и от $n_1, n_2, n_3$, но я так и не смог довести это до конца. Прошу помощи у форумчан.

[--mS--]

Результат первого взвешивания: $X_1=a+b+\varepsilon_1$. Дальше сами.

[maked0n]

--mS-- в сообщении #1156425 писал(а):

Результат первого взвешивания: $X_1=a+b+\varepsilon_1$. Дальше сами.

Насколько я понял, имеется ввиду, что нужно сделать так:
$\\ X_i = a + b + \varepsilon_i, i \in [0, n_1)\\ X_j = b + c + \varepsilon_j, j \in [n_1, n_2),\\ X_k = a + b + c + \varepsilon_k, k \in [n_2, n_3) $
Тогда можно сказать, что $X_m = X_i + X_j + X_k = 2a + 2b + 2c + \varepsilon_i + \varepsilon_j + \varepsilon_k$. Но тогда у меня вопрос: могу ли я сказать, что $\varepsilon_i + \varepsilon_j + \varepsilon_k = \varepsilon_m$ и рассматривать в качестве погрешности теперь только $\varepsilon_m$, таким образом сведя задачу к линейной гауссовской модели (т.е. представив, как $\vec{X} = \vec{l}\cdot\vec{\varepsilon}$)?

UPD: хотя вот сейчас подумал, что наверное можно так:
$ \vec{X} = \begin{pmatrix} 2 & 2 & 2\\ 2 & 2 & 2\\ . & . & .\\ 2 & 2 & 2 \end{pmatrix} \cdot \begin{pmatrix} a \\ b \\ c \end{pmatrix} + \begin{pmatrix} \varepsilon_0 \\ . \\ . \\ \varepsilon_{n_1} \\ . \\ . \\ \varepsilon_{n_2} \\ . \\ . \\ \varepsilon_{n_3} \\ \end{pmatrix} $
Тогда, по-идее, мы уже свели задачу к гауссовской модели. Правильно?

[maked0n]

Или, может быть, вот так:

$$\begin{pmatrix} 1 & 1 & 0\\ ... & ... & ... \\ 0 & 1 & 1 \\ ... & ... & ... \\ 1 & 1 & 1 \end{pmatrix} \cdot \begin{pmatrix} a \\ b \\ c \end{pmatrix} = \begin{pmatrix} \varepsilon_0 \\ ... \\ \varepsilon_{n_1} \\ ... \\ \varepsilon_{n_2} \\ ... \\ \varepsilon_{n_3} \\ \end{pmatrix}$$

?

[--mS--]

maked0n в сообщении #1156472 писал(а):

Или, может быть, вот так:

Конечно, так.

[maked0n]

Спасибо!