Аналог формулы Эйлера-Чаппела для вневписанной окружности

[Rusit8800]

Сама задача(точнее упражнение) из статьи "Кванта" - "Два века теоремы Понселе".Задача состоит в нахождении расстояния между центром описанной окружности и вневписанной.Идей было много, некоторые отрезки я выражал через стороны, где-то использовал теорему косинусов, но все становилось более громоздким и громоздким, короче все эти идеи я забросил.Я не нашел даже полезных подобных треугольников.Была еще идея: пусть $O$-центр описанной окружности, $J_1$-центр одной из вневписанных, а $T_1, T_2$- 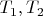точки пересечения этих окружностей, тогда найдя $T_1T_2$, несложно найти $OJ_1$.Однако найти $T_1T_2$,по-моему, не легче чем $OJ_1$(возможно даже сложнее,$T_1T_2$ скорее всего будет очень громоздким).
Можете подсказать направление?