Я слабый вариант напишу, чтобы хоть какой-то ответ был. не успел

Отсюда следует, что

.
Наши числа имеют вид

.

Далее достаточно доказывать равномерность распределения

, т.к. линейное преобразование на равномерность не влияет.
Значения суммы

равномерно распределены на

при

. При

это и так видно, а для остальных

можно доказать по индукции (или по критерию Вейля должно получаться).
Наконец, уравнение

не дает равномерного распределения числа решений по

, но это распределение становится равномерным при

. Это не совсем ясно, но более интуитивно очевидно, чем требуемое утверждение.
Причем значение

- это довольно мало, т.к. ему соответствует всего 2 слагаемых, когда распределение еще не равномерно, надо хотя бы
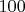
примерно.
При

распределение числа решений вообще равномерно? Кто-нибудь считал?
Пусть

- количество

-значных чисел указанного вида и имеющих остаток

от деления на 7. Тогда для любых

,

и
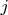
справедливо

.
 .
.Нет, в самом деле - здесь максимальная степень равномерности для всех


Т.е. даже не

, а даже

.