Гильбертовы пространства

[ProPupil]

Пусть $H$ - гильбертовое пространство, а $T: H \to L_2(0,1)$ - линейный оператор.

Докажите, что для оператора $T$ эквивалентны следующие утверждения:

1. Существует отображение $\xi \in L_2(0,1;H)$ такое, что $(Th)[t] = (h, \xi(t))$
2. Для произвольной ортонормированной последовательности $\{e_n\}_{n=1}^\infty \subset H$ верно, что $\sum\limits_{n=1}^\infty \|Te_n\|^2 < \infty.$
3. Существует такая измеримая функция $g \in \mathfrak M(0,1;\mathbb R)$, что для любой функции $f \in T(\bar B_1(0))$ верно, что $\operatorname{mes} \{t \in (0,1): |f(t)| \leq g(t) \} = 1$, где $B_1(0)$ - единичный шар пространства $H$ с центром в нуле.

[sup]

В пункте а) надо бы "для п.в. t".
А пункт с), судя по всему, неверный. Пусть $H = L_2(0,1)$, $T$ --- тождественный. Тогда у всех функций из единичного шара есть общая измеримая мажоранта.
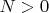
Пусть $N > 0$, $f$ - ступенька высоты $N$ и мера носителя $1/N^2$. Тогда на этом множестве $g(t) \geqslant N$. ИТД.
Может там какое-то доп. условие есть?

[ProPupil]

Тут задача состоит в доказательстве эквивалентности трёх утверждений. То есть, надо доказать, что если выполнено одно из условий a) - c), то выполнены и другие условия.

Для указанного Вами единичного оператора не выполняется условие b), поэтому и остальные пункты не могут быть выполнены.

[sup]

Ага, понял.
Так и знал, что что-нибудь упустил.

[sup]

И все-таки одной измеримости $g(t)$ не хватает. Пусть $H = l_2$. Пусть, далее, $Te_k = \varphi_k(t)$. При этом $\varphi_k(t)$ положительная с единичной нормой, а ее носитель расположен внутри $(\frac {1}{k+1}, \frac {1}{k})$. Тогда
$g(t) = \sum \varphi_k(t)$
А вот условие b), очевидно, не выполнено.
Полагаю, требуется еще и $g(t) \in L_2(0,1)$.

[ProPupil]

Да, согласен. Вы тут правы