Well, "symmetric" means that

. Your condition means that

. Now let's take all combinations of these two (they happen to generate a dihedral group of order 12) and get to the result.
Let

be any polynomial; then

is your

. The obvious implications as to the degree of

I leave to yourself.
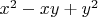
seems to be the "simplest" non-trivial example in some sense.