Солитон на поверхности мелкой воды

[german417]

П.1. Решение уравнения КДВ можно получить спектральным методом.
Вопрос 1: можно ли к полученному спектру синусоидальных бегущих волн применить законы распространения синусоидальных волн на мелкой воде и, суммируя их, получить солитон?

П.2. Известны классические решения уравнения КдВ на основе гиперболической функции sech. Возьмем профиль солитона в сеточной разбивке и вычисляем с помощью БПФ его дискретный спектр. Полученный спектр амплитуд, длин волн и фаз используем для формирования спектра бегущих синусоидальных волн.
Вопрос 2: в принципе, одинаковы ли солитоны (пп.1 и 2), если число спектральных составляющих в обоих спектрах (пп. 1 и 2) одинаково?

[пианист]

german417
Отвечаю по тому, что понял в Вашем тексте.
Решение КдВ общего вида со временем распадается на солитоны.
Суммировать (в обычном смысле, т.е. просто складывать) решения КдВ нельзя, т.к. оно нелинейно, соответственно, разложение Фурье применить к нему тоже нельзя.
Существует процедура суперпозиции решений КдВ, но это не просто сложение.
Бегущие волны КдВ не синусоидальные, а кноидальные.

[Munin]

Картинка для НУШ:



(Ахмедиев, Анкевич. Солитоны.)

[german417]

Да, действительно, это моя ошибка, надо было не только в заголовке, но и в тексте написать, что речь идет о солитоне, т.е об уединенной волне.
То, что Вы написали - верно. Спасибо за внимание к вопросу.
Поэтому ещё раз оговорюсь, речь идет о сравнении двух солитонов, см. П1 и П2 моего вопроса.

[Munin]

Вы можете разложить солитон по синусоидам, но что вы потом с этим разложением будете делать?

Вы понимаете, почему эти фокусы проходят с линейными дифурами, типа Д'Аламбера и Клейна-Гордона?

[german417]

Спасибо за ответ.

Что буду делать. Методом вычислительной гидродинамики (CFD) моделирую солитон. Для этого в качестве граничного условия на входе расчетной области применяю скорости втекающей жидкости по каждой синусоиде спектра. Такие формулы для скорости жидкости синусоидальных волн с учетом мелкой воды в литературе имеются.

Теперь по поводу понимания вопроса. Да понимаю, сомневаюсь, поэтому обратился к литературе. Существует спектральный метод решения уравнения КДВ, в результате применения которого получается спектр синусоид. В качестве примера можно упомянуть статьи:
- Tony F. Chan, Tom Kerkhoven. Fourier Methods with Extended Stability Intervals for Korteweg – de Vries Equation;
- Д. Ф. Сиковский. Методы вычислительной теплофизики.
на стр. 78 Сиковский Д.Ф. пишет: уравнение КдВ можно также решать с помощью спектрального метода, используя разложение в ряд Фурье. Подставляя это разложение в уравнение КдВ, получаем систему уравнений для амплитуд гармоник. Применение спектральных методов в вычислительной гидродинамике подробно описано в книге [Canuto et al., 2006].

Т.е. коль скоро солитон представить можно спектром синусоид, то я взял готовое решение (профиль) солитона и разложил его в ряд Фурье. Затем CFD-методом получил движущийся солитон по поверхности мелкой воды. Все условия уравнения КдВ (высота солитона, глубина канала) разумеется соблюдены.

[Munin]

Цитаты оформляются с помощью тега quote. Формулы записываются в формате LaTeX, в окружении одиночных или парных долларов.

german417 в сообщении #1135048 писал(а):

на стр. 78 Сиковский Д.Ф. пишет:

Цитата:

уравнение КдВ можно также решать с помощью спектрального метода, используя разложение в ряд Фурье. Подставляя это разложение в уравнение КдВ, получаем систему уравнений для амплитуд гармоник.

А вы сами-то его подставляли, получали эту систему уравнений?

german417 в сообщении #1135048 писал(а):

Такие формулы для скорости жидкости синусоидальных волн с учетом мелкой воды в литературе имеются.

Приведите.

german417 в сообщении #1135048 писал(а):

Методом вычислительной гидродинамики (CFD) моделирую солитон.

В смысле, каким-то пакетом пользуетесь, или сами на бумажке пишете выкладки, которые потом программируете?

----------------

Дело в том, что разложить решение по Фурье можно. Но с линейными уравнениями это работает хорошо, а с нелинейными - плохо. Потому что линейные уравнения сами хорошо раскладываются по Фурье. Поясню. Допустим, я имею линейное уравнение, типа

$$a\dfrac{\partial^2}{\partial x^2}f+b\dfrac{\partial}{\partial x}f+cf=\dfrac{\partial}{\partial t}f.$$

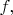
Раскладывая по Фурье не только $f,$ но и применяемые к ней дифференциальные операторы, я получаю

$$a(ik)^2\tilde{f}+b(ik)\tilde{f}+c\tilde{f}=\dfrac{\partial}{\partial t}\tilde{f}$$

- то есть, фактически упрощаю дифференциальное уравнение до алгебраического. Дальше оно и решается как алгебраическое. А теперь возьмём уравнение с какой-нибудь нелинейностью, например,

$$\ldots f^2\ldots\quad\textit{или}\quad\ldots f\dfrac{\partial}{\partial x}f\ldots$$

Тогда после преобразования Фурье мы внезапно получаем:

$$\ldots \tilde{f}\ast\tilde{f}\ldots,\qquad\ldots \tilde{f}\ast(ik\tilde{f})\ldots,$$

где $\ast$ - свёртка. И у нас вместо дифференциального уравнения - интегральное! Хрен редьки не слаще, а даже горше - дифуры решать легче, чем интегральные.

Может, во всём этом есть какой-то удобный вычислительный аспект? Но я о нём не знаю, и навскидку не просматривается...

[german417]

Спасибо за консультацию.