Несобственный интеграл

[Noct]

Задали найти интеграл

$$\int\limits_{0}^{1} \ln(1-x)\ln(x)dx$$

Я разложил логарифм в ряд Тейлора
получил:

$$ - \int\limits_{0}^{1}\sum\limits_{k=1}^{\infty}\frac{x^k}{k}\ln(x)dx$$

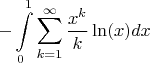
Дальше поменял суммирование и интегрирование и получил:

$$ - \sum\limits_{k=1}^{\infty}\frac{1}{k}\int\limits_{0}^{1}x^k\ln(x)dx $$

Интеграл

$$\int\limits_{0}^{1}x^k\ln(x)dx$$

удалось посчитать по частям получилось:

$$\int\limits_{0}^{1}x^k\ln(x)dx = -\frac{1}{(k+1)^2}$$

Ряд:

$$\sum\limits_{k=1}^{\infty}\frac{1}{k(k+1)^2}$$

удалось преобразовать как

$$\sum\limits_{k=1}^{\infty}(\frac{1}{k} - \frac{1}{k+1}) - \sum\limits_{k=1}^{\infty}\frac{1}{k^2} - 1 = 2 - \frac{\pi^2}{6}$$

Законны ли все операции с несобственными интегралами которые я сделал? B можно-ли было посчитать этот интеграл по другому без разложения логарифма в ряд и тем самым получить еще одно доказательство формулы $\sum\limits_{k=1}^{\infty}\frac{1}{k^2} = \frac{\pi^2}{6}$?

[Padawan]

Все члены одного знака, так что все нормально, все законно.

[SCW]

Noct, Ваш интеграл выражается через элементарный случай Эйлеровой $B$-функции

[Noct]

SCW, Не подскажите как начать действовать чтобы свести к Бета функции? Я полагаю надо сначала по частям прокрутить или что-нибудь добавить/вычесть чтобы 2 появилась.

[SCW]

Noct, продифференцируйте по параметру интегральное представление $B$-функции и перейдите к пределу