karandash_olegЕсли приходится решать много таких задач, как первая, можно это дело рационализировать. Договоримся всё нумеровать с нуля (как поступают настоящие программисты): и перестановки в списке, и позиции цифр в каждой перестановке. Итак, наша перестановка

-я, нумеруя перестановки с нуля.
Запишем число

в
факториальной системе счисления:

По правилам, при

может стоять коэффициент от

до

, при
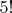
— коэффициент от

до

и так далее, тогда разложение единственно. Для небольших чисел его легко получить вручную.
Итак, у нас есть список коэффициентов

и список цифр

. Делаем так. Берём значение самого левого коэффициента, берём цифру с такой позицией в списке цифр. Коэффициент вычёркиваем из списка коэффициентов, а взятую цифру пишем, и тоже вычёркиваем из списка цифр. Получится:

Цветом выделены цифры, с которыми мы сейчас поработаем и вычеркнем.