Добрый день!
Дано следующее определение подгруппы порождённой подмножеством.
Цитата:
У свободной подгруппы
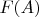
на множестве

есть следующее универсальное свойство: для любой группы

, для любой функции

существует только один гомоморфизм групп

такой, что

, где

- вложение

в
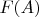
(

).
Далее, подгруппа

группы

определяется так: пользуясь универсальным свойством свободной группы на множестве

получаем, что для функции-вложения

существует гомоморфизм

такой, что

. Имеем: функция

определённая по закону

, где

- либо элемент множества

, либо его обратный, есть гомоморфизм групп. Тогда

. То есть подгруппа, порождённая подмножеством

в группе

, есть образ этого гомоморфизма

.
Далее, необходимо доказать, что группа

является конечно порождённой тогда и только тогда, когда существует сюръективный гомоморфизм

. Очевидно(из определений выше), что если группа конечно порождена, то существует сюръективный гомоморфизм

для некого конечного подмножества

. Допустим

. Тогда существует изоморфизм групп

. И, следовательно, существует сюръективный гомоморфизм

Как быть дальше? Осталось доказать, что если существует сюръективный гомоморфизм групп

, то существует сюръективный гомоморфизм групп

для некого конечного подмножества

, то есть группа

является конечно порождённой.
Думаю, что если существует сюръективный гомоморфизм

, то

, но как это доказать? Далеко не факт, что

, то есть не факт, что

.