Решить систему в натуральных числах:

В ответе к задачке сказано ,что

.Их решение понятно, но в моем решении я не могу найти ошибку.


Из данной системы следует уравнение:




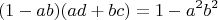


Однако данное уравнение допускает другое решение, скажем

Скажите, где я не прав.
-- 03.06.2016, 13:18 --Ой,


Может есть надежда, что мое решение правильное?
 -- 03.06.2016, 13:22 --
-- 03.06.2016, 13:22 --Да, оно допускает, только что

, если

.Можете удалять тему.