Наибольшее значение функции

[GevorgyanH1]

Нужна помощь. Найти наибольшее значение функции $z=x+y$ в области, координаты точек которой удовлетворяют условию $(y^2-(x-1)^4)\sqrt{6x-x^2-y^2} <= 0$.

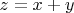
Проще говоря, ищем максимум $z$ на границе круга (первый множитель ничего не решает). Мне не ясно, как это делать. Вроде бы все просто. Можно ли тут методом множителей Лагранжа воспользоваться, имея в виду $z = x+y$ при условии $(x-3)^2+y^2 \le 9$ ?

[Mihr]

GevorgyanH1 в сообщении #1125427 писал(а):

Проще говоря, ищем максимум $z$ на границе круга (первый множитель ничего не решает)

В каком смысле "ничего не решает"? Этот множитель тоже имеет значение. Область, заданная приведённым Вами неравенством, - не круг, а лишь его часть.
А захотите Вы воспользоваться методом множителей Лагранжа или предпочтёте выразить одну переменную через другую - это уже дело вкуса.
Можно порекомендовать также построить ряд линий уровня - это серьёзно облегчает анализ задачи.