Vietnamese system

[ins-]

Solve the system:
$x\sqrt{x-y}+y\sqrt{x+y}=xy$
$x\sqrt{y-1}+y\sqrt{x-1}=x+y$

[12d3]

ОДЗ: $ x \ge y \ge 1$
$xy = x\sqrt{x-y}+y\sqrt{x+y} = \left(x\sqrt{x-y}-(x-y)\sqrt{2y}\right)+\left(y\sqrt{x+y}-y\sqrt{2y}\right)+x\sqrt{2y} =$
$= \sqrt{x-y}\left(x-\sqrt{2y(x-y)}\right) + y\left(\sqrt{x+y}-\sqrt{2y}\right) + x\sqrt{2y} = $
$= \sqrt{x-y}\frac{x^2-2y(x-y)}{x+\sqrt{2y(x-y)}} + y\left(\sqrt{x+y}-\sqrt{2y}\right) + x\sqrt{2y} = $
$=\sqrt{x-y}\frac{(x-y)^2+y^2}{x+\sqrt{2y(x-y)}} + y\left(\sqrt{x+y}-\sqrt{2y}\right) + x\sqrt{2y} \ge x\sqrt{2y}$, т.к первые два слагаемых неотрицательны.
Следовательно $\sqrt{y} \ge \sqrt{2}$ и $y \ge 2$
При $x \ge y \ge 2$ получим $x\sqrt{y-1} +y \sqrt{x-1} \ge x\cdot 1+y \cdot 1 = x+y$, причем равенство достигается только при $x=y=2$. Подставив в первое уравнение, выясним, что $x=y=2$ действительно корни.

[waxtep]

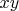
1. $x\ge y\ge 1$ to keep roots positive; let us divide second equation by $xy$ and group:

$$\frac {\sqrt {x-1}-1} x + \frac {\sqrt {y-1}-1} y =0$$

This means that $y \le 2\le x$ and gives one solution $x=y=2$.
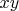
2. now let's also divide first equation by $xy$ and take $x=ky, k\ge 1$:

$$\sqrt {k-1}+\frac {\sqrt {k+1}} k=\sqrt y$$

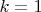
It gives $y=2$ for $k=1$, and there goes a tedious proof that it is a minimum for all possible values of $k$ (I'm not sure that it is of interest, basically a proof that $k^2\sqrt {k+1}> (k+2)\sqrt {k-1}$ for $k\ge 1$). So no other solution except $x=y=2$ is possible, as we know that $y\le 2$ from $(1)$.

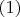
-- 21.05.2016, 08:57 --

...and the proof of $\sqrt {k-1}+\frac {\sqrt {k+1}} k\ge \sqrt 2$ can be done simply: $\sqrt {k-1}+\frac {\sqrt {k+1}} k \ge \sqrt {k-1}+\frac {\sqrt 2} k$, so taking $k=1+t$ we need to prove $\sqrt \frac t 2 \ge \frac t {1+t}$, which is clear.

[ins-]

Thank you guys for the excellent solutions! For the collection I'm posting one more link.
http://artofproblemsolving.com/communit ... 46p6382537