Gibbs phenomenon

[druggist]

Хотелось бы услышать простое объяснение феномена Гиббса (Gibbs phenomenon), что называется, "на пальцах", дабы "почувствовать" суть эффекта.

[Pphantom]

Тема перемещена из форума «Помогите решить / разобраться (Ф)» в форум «Помогите решить / разобраться (М)»
Причина переноса: явление Гиббса (кстати, по этому словосочетанию гуглится ворох разнообразных объяснений, в т.ч. и весьма доходчивых) никакого отношения к физике не имеет.

[Brukvalub]

См. раздел Explanation в статье по вашей ссылке.

[timber]

Мы этот "феномен" проходили в университете на курсах теории электрической связи и цифровой обработки сигналов.
Попробую объяснить Вам.
Возьмем, допустим, какой-то вид информации. Ну, например, графическую или изображение.

Физическая часть
Передача и хранение информации осуществляется с помощью различных знаков (символов), которые позволяют представить её в некоторой форме.

Ну, например, Вы там что-то рисуете/записываете какими-то символами -- кружочками, линиями, ну вообщем, как Вам в голову взбредет.
Получили рисунок. Потом решили передать/показать его Вашему другу, который находится за 1000 км. от Вас.
Это в простой форме. В более современном варианте -- решили устроить онлайн мастер-класс Вашей классной техники рисунка.
Сообщение это совокупность знаков, отображающих ту или иную информацию.

Передача сообщений (а, следовательно, и информации) на расстояние осуществляется с помощью какого-либо материального носителя, например, бумаги или магнитной ленты или физического процесса, например, звуковых или электромагнитных волн и т.д.
Сигнал это физический процесс с помощью которого передается сообщение. Сигнал передаёт (развёртывает) сообщение во времени, то есть всегда является функцией времени. Сообщения могут быть функциями времени, например речь при передаче телефонных разговоров, футбольный матч при передаче по телевидению и т.п., но могут и не является функцией времени (например, картинка/неподвижное изображение и т.д.).
Сигнал передаёт сообщение во времени. Следовательно, он всегда является функцией времени, даже если сообщение (например, неподвижное изображение) таковым не является.
Нас интересует передача сообщения на расстояние с помощью электромагнитной волны. Как известно, волна -- это колебания, распространяющиеся в пространстве в течении времени, т.е. колебательный процесс.

Математическая часть.
Так вот. Числовой (цифровой) эквивалент колебательного процесса -- это бесконечная сумма вида:
$1 - 1 + 1 - 1 + 1 - 1 + ...$

Чему равна эта последовательность/сумма? Это большой вопрос!

Если мы воспользуемся обычными правилами конечной арифметики, то получим разные результаты.
Возьмем ассоциативный закон и применим к данной последовательности:
$(1 - 1) + (1 - 1) + (1 - 1) + ... = 0 + 0 + 0 + ... = 0$
$1 + (-1 + 1) + (-1 + 1) + ... = 1 + 0 + 0 + ... = 1$
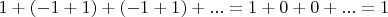
Математики долго бились над этим вопросом и пришли к выводу (еще во времена Лейбница и Эйлера), что сумма будет $1/2$.

Есть два основных понятия при изучении числовых рядов -- это частичная сумма и сходимость.
Частичная сумма -- это нарастающая сумма (начиная с первого) конечного числа элементов ряда.
Например, для указанного ряда, первые 4 частичные суммы:
$S_1 = 1, S_2 = 1 - 1 = 0, S_3 = 1 - 1 + 1 = 1, S_4 = 1 - 1 + 1 - 1 = 0$
Видно, что частичные суммы скачут (0 и 1, 0 и 1).
В этом случае говорят, что последовательность (ряд) не сходится или по-другому, частичные суммы ряда по мере увеличения числа членов не стремятся к какому-то определенному (предельному) значению.
Рассмотрим другую последовательность чисел:
$1 - 1/2 + 1/3 - 1/4 + 1/5 - 1/6 + ...$
Такой ряд уже сходится (можете проверить сами). К определенному конкретному значению.

Вроде бы все отлично. Но нет!

Сходящийся ряд тоже с сюрпризом. Если переставить члены такого ряда в другом порядке, то получится другое значение к которому сходится ряд. То есть данную последовательность можно подвести к любому числу.

Какая тут связь с нашими электромагнитными сигналами?
Как известно основным/базовым представлением электромагнитной волны (колебания) является синусоида или косинусоида.
Был такой математик по фамилии Фурье, который показал, что практически любая сложная форма волны может быть представлена как сумма простых волн. Анализ Фурье -- это метод представления сложной функции суммой простых составляющих (гармоник) -- синусоид и косинусоид, поэтому анализ Фурье известен также под названием «гармонический анализ». Соответствующая сумма гармоник называется рядом Фурье.
Вот тут интересно написано: https://habrahabr.ru/post/219337/.

Сходимость ряда Фурье -- это тоже большой вопрос! Тут тоже есть сюрпризы.

Например, рассмотрим один из рядов Фурье:
$f(x) = \sin(x) - 1/2 \sin (2x) + 1/3 \sin (3x) - 1/4 \sin (4x) + ...$
Частичная сумма первых 10 членов такого ряда изображена в виде графика:

В идеальном случае синусоида должна приблизиться вплотную к более простой кривой в форме зубцов волны (показана пунктиром).
Но видно, что при изменении направления (когда график переходит вниз) синусоида ведёт себя странным образом -- удаляется от пунктирной линии.
Ученые пытались избавиться от такого "всплеска" путем включения в частичную сумму большего числа слагаемых, но безуспешно.
Всплеск становится тоньше и просто перемещается ближе к точке перегиба.

Частичная сумма первых 50 членов такого ряда изображена в виде графика:


Показанный эффект -- всплеск на краях обычно называют явлением/феноменом Гиббса.
Такие нежелательные всплески приводят к размытости, мерцанию, квадратикам и прочим искажениям на краях, например, изображения при передаче сигнала по сетям связи.
Ваш друг не может чётко разобрать у себя на видеоизображении какие-то нарисованные Вами элементы. Или получил Вашу картину, но места перехода цвета красок оказались размыты или вообще другого (черного!) цвета, хотя такими они не были на Вашем исходном рисунке. Вы черный цвет вообще не использовали.
Вот такие сюрпризы!
Но их уже научились фильтровать.

PS. Не знаю, стало ли что-то понятнее и "почувствовали" ли Вы эффект.

[druggist]

Спасибо за развернутый ответ

timber в сообщении #1123378 писал(а):

PS. Не знаю, стало ли что-то понятнее и "почувствовали" ли Вы эффект.

Пока нет, но постараюсь

[ewert]

druggist в сообщении #1123343 писал(а):

Хотелось бы услышать простое объяснение феномена Гиббса

Этот вопрос распадается на два: 1) почему этот эффект вообще возможен, т.е. почему ему не следует удивляться и 2) почему наблюдается именно он.

Ответ на первый вопрос очень прост. Ряд Фурье для разрывной функции не может сходиться к этой функции равномерно, т.к. при равномерной сходимости ряда, составленного из непрерывных функций, его сумма также непрерывна. Неравномерность же может проявляться как угодно; и, в частности, амплитуда "паразитных" колебаний частичных сумм вовсе не обязана стремиться к нулю. Стягиваться к точкам разрыва эти колебания обязаны, а вот их размах -- уменьшаться не обязан. Ну он и не уменьшается.

А вот ответ на второй вопрос -- почему этот размах фактически не уменьшается и, более того, стремится к некоторому вполне определённому пределу -- требует уже конкретного счёта. Почему вообще в нормальной ситуации ряд Фурье сходится к раскладываемой функции? -- Потому, что значения его частичных сумм для каждой точки $x$ представляют собой некоторый вполне явный интеграл:

$$S_n(x)=\int_0^{2\pi}f(t)\cdot D_n(x-t)\,dt,$$

т.е. свёртку с т.наз. ядром Дирихле $D_n(x)=\frac{\sin\frac{(2n+1)x}{2}}{2\pi\sin\frac{x}{2}}$. Для него характерны 1) всё более частые осцилляции ядра с ростом номера и 2) равенство единице интеграла по всему периоду от самого ядра. За счёт первого существенный вклад в свёртку даёт лишь малая окрестность точки $x$, т.е. интеграл по остальной части периода стремится к нулю, сколь бы малой эта окрестность ни была. Поэтому если $x$ -- точка непрерывности, то интеграл стремится к $f(x)$, умноженному на единицу, т.е. на интеграл от просто ядра (ну там надо ещё, конечно, наложить на раскладываемую функцию некоторые доп. требования, но они не принципиальны).

Если же мы имеем дело с точкой разрыва $x_0$, то функцию можно представить как сумму непрерывной в этой точке плюс функция, равная некоторой симметричной ступеньке $\chi(t-x_0)$ в окрестности этой точки, а дальше уже не важно. Интеграл от первого слагаемого сходится равномерно, так что весь эффект сводится к интегралу от второго. Для второго же слагаемого ядро Дирихле можно заменить на его асимптотическое поведение в окрестности $x$, т.е. на $\frac{1}{\pi(t-x)}\sin\frac{(2n+1)(t-x)}{2}$, а пределы интегрирования и ступеньку распространить на всю ось (поправки будут равномерно стремиться к нулю опять же в силу учащения осцилляций). Т.е. частичная сумма ряда представляет собой сумму некоторого равномерно сходящегося слагаемого и вполне конкретного интеграла

$$\int_{-\infty}^{+\infty}\chi(t-x_0)\cdot\frac{1}{\pi(t-x)}\sin\frac{(2n+1)(t-x)}{2}\,dt,$$

а это (с точностью до всяких множителей и замен) -- просто интегральный синус. Вот его график и даёт предельную картинку для эффекта Гиббса (по Вашей ссылке соотв. картинки приведены в разделе Signal processing explanation).

[profrotter]

Самое простое объяснение на пальцах: в частотной области ограничение спектра можно рассматривать как прибавление, начиная с некоторого значения частоты, такого же как и у сигнала "хвоста" спектра, но с отрицательным знаком. К сигналу при этом следует прибавить высокочастотную пульсацию, соответствующую прибавленному при усечении спектру. Это, конечно, не поясняет, почему с увеличением частоты усечения максимальный размах пульсаций не уменьшается.

Ах, ну и ещё там, где разрыв, в описании (непериодического) сигнала присутствует функция Хевисайда, которая при ограничении спектра превращается в что-то вида $\int\limits_0^t sinc(ax)dx$ (свёртка функции Хевисайда и обратного преобразования Фурье от прямоугольной функции).

[ewert]

(Оффтоп)

есть ещё третье объяснение: не исключено, что ТС просто не понимал, в чём, собссно, эффект. В таком случае третье (т.е. нулевое по модулю три) объяснение timber было как раз наиболее уместным, мы же вмешались вовсе и некстати.

[druggist]

Мне вот это объяснение показалось наиболее ясным и доступным:
https://mipt.ru/education/chair/physics/upload/5c5/Gibbs_txt-arph8mld9gb.pdf
Кроме того в интернете можно найти визуализации типа "circle on circle"

Цитата:

Matthen объясняет трюк Фурье, используя круги вместо синусоид. На помощь ему приходит набор кругов различных размеров, центр каждого из которых находится на границе большего круга. Круги начинают вращаться, маленькие движутся вокруг больших и делают это быстрее. Если проследить движение одной точки на наименьшей окружности, можно реконструировать волну любой формы, как показано на анимации и на картинке. Опять же, преобразование Фурье говорит нам, как построить волну: какие круги и скорости использовать. ...

https://habrahabr.ru/company/achiever/blog/204956/
(см. также: https://www.youtube.com/watch?v=R5SLHTSz1Uc, http://toxicdump.org/stuff/FourierToy.swf)
Мне кажется, overshoot, т.е., конечный выброс над ступенькой, суть явления Гиббса легко пояснить, используя эту визуализацию. Пусть мы стартуем из крайне правого положения точки кружка наименьшего диаметра (в этот момент центры всех кружков выстроились в линию по оси абсцисс. Пусть имеется малый(в пределе $N $ стремящемся к бесконечности) бесконечно малый промежуток времени $\delta t$ . Тогда угловое перемещение точки кружка наименьшего диаметра будет $(2N-1)\delta t$ В максимальном по оси ординат положении эта точка будет, когда этот угол будет равен $\pi$ (в этой точке касательная к кривой будет горизонтальна) Далее, подставляем эту $\delta t$, выраженную через $N$ в $S_N(t)$ - сумму первых $N$ ненулевых членов ряда Фурье, и, далее, как и в вышеприведенном пособии Булыгина В. С. , заменяя суммирование интегрированием, приходим к интегральному синусу.