Здравствуйте. Рассматривается уравнение теплопроводности в прямоугольнике с граничными условиями второго рода.
При постановке граничных условий в литературе встречаются обозначения

и
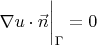
, где

- искомая функция,

- внешняя нормаль к границе

области (прямоугольника).
Объясните, пожалуйста, в чем разница между ними? Взаимозаменяемы ли они?