Приближение сильной связи в ФТТ

[doun]

Доброго времени суток!

Прошу помочь разобраться с приближением сильной связи используемым при вычислении зонной структуры в фтт. Я нигде в литературе не могу найти примера вычисления энергии зоны образованной состояниями с вырожденой энергией. Теперь конкретно вопрос. Основываясь на системе уравнений для энергии зоны приведенной в книге Н. Ашкрофта "Физика твердого тела", Том 1 (год издания не указан у меня в электронной версии), уравнение (10.12), стр. 184. Если ввести обозначения $E(\mathbf{k})-E_n=\lambda$,

$\gamma_1^{n,m}=\sum\limits_{\mathbf{R}\ne0}e^{i\mathbf{k}\mathbf{R}}\int\psi_{m}^*(\mathbf{r})\psi_{n}(\mathbf{r}-\mathbf{R})d^3R$

$\gamma_2^{n,m}=\sum\limits_{\mathbf{R}\ne0}e^{i\mathbf{k}\mathbf{R}}\int\psi_{m}^*(\mathbf{r})\triangle V(\mathbf{R})\psi_{n}(\mathbf{r}-\mathbf{R})d^3R$

$\gamma_3^{n,m}=\int\psi_{m}^*(\mathbf{r})\triangle V(\mathbf{R})\psi_{n}(\mathbf{r}-\mathbf{R})d^3R$

то в них уравнение (10.12) примет вид:

$\lambda\mathbf{b}=\left(1+\gamma_1\right)^{-1}\left(\gamma_3+\gamma_2\right)\mathbf{b}$

Теперь получается, что определение зонной структуры сводится к решению задачи на с.з. и с.в.
матрицы

$M=\left(1+\gamma_1\right)^{-1}\left(\gamma_3+\gamma_2\right)$

Теперь если уровень $E_n$ $s$ кратно вырожден то матрица $M$ будет размерностью $s\times s$, а ее элементы будут составляться из волновых функции относящихся к значению энергии $E_n$.
Я правильно все понимаю?

Заранее благодарен.

[Munin]

У вас формулы перевраны. В Ашкрофте-Мермине (Мермин обижается, что вы его забыли) интегралы по $\mathbf{r}$ малому, что существенно, поскольку он входит в аргументы всех подынтегральных функций.

Ваша матрица имеет индексы $m,n.$ Они пробегают все атомные орбитали (участвующие в расчёте). Если среди них есть вырожденные - то они все должны быть учтены по отдельности, конечно же. Но не только они - их недостаточно.

[doun]

Они не перевраны, это просто опечатка, не досмотрел (сейчас уже нет возможности исправить, или же я не знаю как). Меня не интересуют атомные орбитали. У меня вопрос: есть набор в.ф. описывающих какую то систему с энергиями $E_n$, каждое значение энергии $s$ кратно вырождено. Все энергетические уровни расположены на достаточном расстоянии друг от друга, так, что расстояние между зонами пораждаемыми этими уровнями тоже достаточно велико. И теперь мой первоначальный вопрос. Каким уравнением будет определяться зонная структура?

[Munin]

doun в сообщении #1119055 писал(а):

Все энергетические уровни расположены на достаточном расстоянии друг от друга, так, что расстояние между зонами пораждаемыми этими уровнями тоже достаточно велико.

Учитывать соседние уровни необходимо для того, чтобы уровни вообще расплывались в зоны. На языке волновых функций: у вас перекрываются волновые функции соседних атомов (иначе не будет зонной структуры), и вот эти перекрытия создают поправки к волновым функциям отдельных атомов. Эти перекрытия необходимо разложить по какому-то базису, пусть и приближённо. Одними только вырожденными орбиталями вы тут не обойдётесь - потому что даже для двух атомов новые энергии должны оказаться больше и меньше исходного уровня (при чётной и нечётной комбинации орбиталей).

-- 28.04.2016 19:25:33 --

doun в сообщении #1119055 писал(а):

Каким уравнением будет определяться зонная структура?

Кроме этого момента, кажется, уравнение вы составили верно.

-- 28.04.2016 19:27:15 --

(Оффтоп)

doun в сообщении #1119055 писал(а):

сейчас уже нет возможности исправить, или же я не знаю как

Время редактирования сообщений составляет 1 час. После этого, можно обратиться к модераторам (жалобой на своё собственное сообщение), и они могут перенести тему или сообщение в "Карантин", где вы его можете редактировать неограниченно, но никто не сможет писать в тему новых сообщений. Кроме того, по мелочи модераторы могут по вашей просьбе отредактировать в сообщении что-то сами.

[doun]

Munin

я не понимаю о чем вы? Как написано в указанной мной книге: "энергия $E(\mathbf{k})$ близка к какой либо энергии $E_n$, а все коэффициенты $b_m$, кроме соответствующих этому уровню и уровням имеющим равную с ним (или близкую) энергию, обязаны быть малыми." Соответственно, в описанном мной случае суммирование в формуле (10.12) будет проводится только по вырожденным состояниям. Или я в чем то не прав?

Должен сказать, что меня интересует не твердое тело, а сам метод сильной связи.

[Munin]

Обязаны быть малыми - это не значит, что они могут быть вообще нулевыми. Если вы их положите нулевыми, то вы расширения уровня в зону вообще не получите.

В каком контексте вас интересует метод сильной связи? Если у вас зоны нет, то вы правы. А если есть (например, в жидкости) - то всё-таки нет.

[doun]

Munin, послушайте, если интегралы перекрытия не малы то и приближение сильной связи не работает. Еще раз, меня интересует случай когда эти самые интегралы малы, включая интегралы перекрытия относящиеся к разным энергетическим уровням.
Контекст может быть разный - какой-то периодический потенциал и необходимо найти в.ф. и т.п. частицы в таком потенциале. Характерный "радиус" потенциальной ямы (как и квадрат модуля в.ф. описывающей состояние "подбарьерной" частицы любого энергетического уровня) достаточно мал по сравнению с "расстоянием" между ямами, т.е. приближение сильной связи работает.
Теперь почему у меня возникли сомнения по поводу уравнения на с.з. для определения зонной структуры вырожденных состояний, которое я привел выше. В этой же книге на странице 164 (задача в) приводится система для определения р-зоны в г.ц.к решетке. И из уравнения что я привел вовсе не следует система уравнений приведенная в книге. 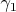Авторы перед первой задачей приводят систему уравнений для определения р-зоны кубических кристаллов и там поясняют, что они выбрасывают множитель $\gamma_1$, но не понятно (по крайней мере мне) они его не учитывают для всех нижеследующих задач?
Поэтому я и решил переспросить.

[Munin]

doun в сообщении #1119371 писал(а):

Munin, послушайте, если интегралы перекрытия не малы то и приближение сильной связи не работает.

Они малы. Но не нулевые. Порядок малости этих интегралов задаёт ширину зоны.

[doun]

Munin
Вы прямо таки открыли мне глаза! А я думал чем же определяется ширина зоны...
Не хочу показаться грубым но у меня складывается ощущение, что вы мне просто морочите голову, постоянно повторяя очевидные вещи.
Тему можно закрывать.

[Munin]

Если вам эти вещи очевидны, то почему вы предлагаете эти интегралы вообще занулить?