Кол-во отображений n-элементного мн-ва на m-элементное мн-во

[m_kristy]

Сколько существует отображений n-элементного множества A на m-элементное множество B.
Решение:
Если $n<m$, то $D_n^m=0$.
Если $n=m$, то $D_n^m=A_n^n$.
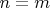
Если $n>m$, то тут уже сложнее.
Вообще всего отображений n-элементного множества в m-элементное множество равно $D_n^m=n^m$, но среди них есть и такие отображения, которые не являются сюръективными. Попробуем их вычесть.
$D_n^m=n^m-m(m-1)^n$. Последнее слагаемое – это количество всех отображений, в которых не задействован ровно один элемент из B, плюс удвоенное количество отображений, в которых не задействованы два и более элементов из B. Получается, что мы вычли лишнее. Вернем часть обратно.
$D_n^m=n^m-m(m-1)^n+C_m^2(m-2)^n$. Последнее слагаемое – это количество отображений, в которых не задействованы ровно два элемента из B плюс утроенное количество отображений, в которых не задействованы три и более элементов из B. Опять прибавили лишнее. Дальше рассуждаем аналогично.
В итоге получаем
$D_n^m=C_m^0n^m-C_m^1(m-1)^n+C_m^2(m-2)^n+...+(-1)^mC_m^m(m-m)=\\=\sum\limits_{i=0}^{m}(-1)^iC_m^i(m-i)^n.$
Правильно? И если правильно, то сойдет такое обоснование?

[provincialka]

m_kristy в сообщении #1118204 писал(а):

Вообще всего отображений n-элементного множества в m-элементное множество равно $D_n^m=n^m$,

Наоборот, $m^n$, у каждого из $n$ элементов есть $m$ возможностей.
Кстати, не стоит одно и то же обозначение $D_n^m$ использовать в разных смыслах: и как число всех отображений и число сюръекций.

[m_kristy]

provincialka, спасибо. А ответ правильный?

[svv]

Вы можете сами проверить:

Цитата:

В комбинаторике числом Стирлинга второго рода из $n$ по $m$, обозначаемым $S(n, m)$ или $\textstyle \lbrace{n\atop m}\rbrace$, называется количество неупорядоченных разбиений $n$-элементного множества на $m$ непустых подмножеств.
...
$S(n, m) = \frac{1}{m!}\sum\limits_{j=0}^m(-1)^{m+j}\;C_m^j\;j^n$

Я чуть приблизил в цитате обозначения к Вашим.
Оставшиеся различия между Вашей формулой и «википедической» объясните, либо покажите, что они несущественны.