Пусть
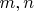
- натуральные числа, требуется доказать следующее неравенство:

, где

- колмогоровская сложность,

- константа, логарифм, естественно, двоичный.
Собственно, что можно сказать прямо сходу про эту ситуацию:
1)

(Это обычное неравенство про модуль)
2)

(Длина натурального числа в двоичной записи)
3) Поскольку процесс вычисления модуля от разности двух натуральных чисел можно вычислить с помощью некоторого алгоритма, то тогда можно записать следующую цепочку неравенств:

Дальнейший ход мысли мне не совсем ясен, ничего путного сходу из данных неравенств сконструировать не удается, значит надо обращаться к определнию колгомоговской сложности и пытаться подкрадываться к оценку через различные алгоритмы описания, возможно это сработает.
Прошу указать направление в котором нужно двигаться, потому как в этой теме я абсолютный новичек и потому пока не имею интуиции, подсказывающей верные идеи.