О свойствах аболютно непрерывных функций

[Evgenii2012]

Уважаемые коллеги ! Предлагается доказать, что непрерывные функции ограниченной вариации, сохраняющие меру нуль, абсолютно непрерывны.
Если кто решал такую задачу, прошу подсказать

[Brukvalub]

Эту задачу решали Банах с Зарецким, поэтому она и называется т. Банаха-Зарецкого.

[Evgenii2012]

Большое спасибо, я нашёл ссылку в книге Натансона - думаю, что вопрос исчерпан

[Dan B-Yallay]

(Оффтоп)

Brukvalub в сообщении #1110378 писал(а):

Эту задачу решали Банах с Зарецким,

Я не помню таких участников на форуме... А кто им помогал то?

[DeBill]

Можно попробовать примерно так (это - не решение, а только набросок)
1. Представить функцию как разность двух монотонных, и проверить для каждой выполнение "сохраняет"..
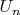
2. Для монотонной: от противного. Пусть для некоторого $\varepsilon >0$ для любого $n$ найдется система $U_n$ из непересекающихся отрезков суммарной длины, меньшей $2^{-n-1}$, образы которых имеют суммарную длину больше $\varepsilon$. Составим новую систему $V_n$, в которую включим все отрезки всех $U_k, k>n$, их суммарная длина тоже мала. Система $V_n$ - вложенная, их образы - тоже, причем суммарная длина образов не мала. Пересечение этих $V_n$ - множество меры 0, а его образ - положительной меры...
Можно также посмотреть книжку Рисс, Сёкефальви-Надь "Лекции по ФА"