Независимость последовательности с.в.

[lofar]

Подскажите пожалуйста, есть ли какая-нибудь теория по следующему вопросу.

Имеются последовательность

$$\xi_1,\;\xi_2,\ldots$$

независимых случайных величин и семейство борелевских функций

$$(f_n|n\in{\mathbb N}),\quad f_n\colon{\mathbb R}^n\to{\mathbb R}$$

.
При каких условиях случайные величины

$$\xi_1,\;f_1(\xi_1)\xi_2,\;f_2(\xi_1,\xi_2)\xi_3,\ldots$$

также будут независимыми?

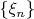
В особенно важном для меня случае, когда $\{\xi_n\}$ --- последовательность независимых одинаково распределенных симметричных бернуллиевских величин: $P(\xi_n = -1) = P(\xi_n = 1) = 1/2$, и f_n(\pm 1,\ldots, \pm 1)=\pm 1 (то есть $f_n(\{-1,1\}^n)\subseteq\{-1,1\}$), новые величины будут независимы.

Если $\xi_1$, $\xi_2$ --- независимые одинаково распределенные бернуллиевские величины: $P(\xi_n = -1) = p$, $P(\xi_n = 1) = q и $f_1(x) = x$, то новые величины $\xi_1,\;\xi_1\xi_2$ будут независимыми если и только если $p=q=1/2$.

Интересно, что будет в общем случае.

[lofar]

Пусть $\{\xi_n\}$ --- последовательность независимых одинаково распределенных симметричных бернуллиевских величин: $P(\xi_n = -1) = P(\xi_n = 1) = 1/2$. И пусть $f_n,\; n=1,2,3,\ldots$ --- произвольный набор функций таких, что $f_n$ --- функция от $n$переменных, принимающая только 2 значения $-1$ и $1$. У меня получилось, что новая последовательность случайных величин

$$\xi_1,\:f_1(\xi_1)\xi_2,\:f_2(\xi_1,\xi_2)\xi_3,\ldots\qquad (1)$$

будет также последовательностью независимых одинаково распределенных симметричных бернуллиевских величин.

Я не специалист по теории вероятностей. Очень хочется услышать мнение экспертов --- возможно я ошибаюсь, возможно случайные величины образующие последовательность (1) зависимы?

Задача возникла всвязи со следующим заданным мне вопросом. "В случайном блуждании, зная все перемещения частицы до заданного момента, можно ли, используя эту информацию, как-то "подправить" знак перемещения в настоящий момент чтобы новое "подправленное" блуждание не колебалось около 0, а уходило к $+\infty$?" Я ответил, что это невозможно и в качестве аргумента привел указанные выше рассуждения. Правильно ли я понял вопрос и правильно ли я ответил --- прошу специалистов высказать свое мнение.

[Dan_Te]

Интересная задача, надо подумать.

[PAV]

По-моему, все правильно. Действительно, величины (1) независимы при любом выборе функций.