В какое наибольшее количество цветов можно покрасить...?

[Ktina]

а) В какое наибольшее количество цветов можно покрасить клетки таблицы $4\times 4$ так, чтобы для любых двух различных цветов нашлись клетки этих цветов, имеющие общую сторону?

б) В какое наибольшее количество цветов можно покрасить клетки таблицы $4\times 4$ так, чтобы для любых двух (не обязательно различных) цветов нашлись клетки этих цветов, имеющие общую сторону?

[lopkityu]

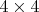
Каждому внутреннему единичному отрезку решетки $ 4\times 4 $ соответствует пара цветов, в которые окрашены клетки, разделенные этим отрезком. То есть, количество различных пар из $ n $ цветов не может превышать количество этих внутренних отрезков, откуда вытекают неравенства $ C_{n}^2\leq 24 $ для первого случая и $ C_{n}^2+n\leq 24 $ - для второго. Имеем оценки $ n\leq 7 $ и $ n\leq 6 $, соответственно, которые можно реализовать такими, например, способами:

$ \begin{array}{llll} 1 2 4 1 \\ 3 6 7 5 \\ 5 4 1 6 \\ 2 3 7 2 \end{array} \begin{array}{llll} 3 1 6 6 \\ 4 1 2 3 \\ 4 5 2 3 \\ 6 5 4 5 \end{array} $

[Ktina]

lopkityu
Спасибо!