Найти площадь цилиндрической поверхности

;
![$\varphi\in [0; \pi/2]$ $\varphi\in [0; \pi/2]$](https://dxdy-02.korotkov.co.uk/f/9/a/0/9a05feca3c3ab25b534ec9b4186bbcc982.png)
, ограниченной плоскостью z=0 и поверхностью

Решаю так:



===============
задача 2
Найти статический момент относительно плоскости z=0 тела, ограниченного поверхностями

, если плотность задана ф-цией

Решаю так:





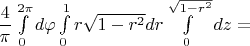

тут думаю уже ошибка.
как понимаю, что-то я тут напутал или не понял, но не могу понять что. спасибо