Прямая

[kfkfkf]

На прямой отмечены несколько (конечное число) точек так, что для любых двух из них найдется третья (тоже отмеченная), такая, что одна из этих трех точек является серединой отрезка между двумя другими. Какое наибольшее количество точек может быть отмечено?
Предполагаемый ответ - 5, (есть пример), но как доказать, что больше нельзя - в голову не приходит

[Karan]

Тема перемещена из форума «Computer Science» в форум «Олимпиадные задачи (М)»

[hippie]

5 точек — правильный ответ.

Введём систему координат так, чтобы крайние точки имели координаты -1 и 1. Тогда этому множеству принадлежит и точка 0.
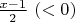
Предположим, что в этом множестве есть точка $x>0.$ Тогда в нём лежат также точки $\frac {x-1} 2\ (<0)$ и $\frac {x+1} 4 (>0).$
Если $x\ne \frac 13,$ то это множество содержит бесконечную последовательность $(a_n)$, в которой $a_0 =x;\quad a_{n+1}=\frac {a_n+1} 4.$