Всем доброго времени суток. Уважаемые плз помогите понять задачу. Металлический диск радиусом

вращается вокруг своей оси с угловой скоростью
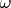
. Найти:
1. напряженность электрического поля

в диске
2. показания вольтметра

, соединенного с контактами, один из которых касается диска в центре, а другой — с краю.
Решение:
1. здесь вроде понятно. Центростремительную силу, удерживающую разлетающиеся к периферии электроны при вращении диска, обеспечивает электрополе, создаваемое ушедшими со своих мест электронами и обеднившими область у центра диска. В результате образуется электрополе

с зарядом

в центре диска и

на периферии. На каждый электрон действует сила Кулона (она же центростремительная):

, где:

- масса электрона. Отсюда находим:

.
2. здесь не понятно. Потенциал на расстоянии

от центра (на периферии):

. Не понимаю как найти потенциал в центре. Ведь в центре находится избыточный заряд

и к нему добавляется потенциал от периферии кольца

. Подскажите плз.