Термодинамика

[Login845]

Изменение внутренней энергии идеального одноатомного газа - это $\Delta U = \frac{3}{2}\Delta pV$ или $\Delta U = \frac{3}{2} p \Delta V $ ?

[DimaM]

На изохоре первое, на изобаре второе.

[Pphantom]

DimaM в сообщении #1099707 писал(а):

На изохоре первое, на изобаре второе.

А в общем случае - еще что-нибудь другое.

[DimaM]

Pphantom в сообщении #1099710 писал(а):

А в общем случае - еще что-нибудь другое.

(Оффтоп)

А в общем случае - сумма.

[Pphantom]

(Оффтоп)

DimaM в сообщении #1099715 писал(а):

А в общем случае - сумма.

Конечные приращения и дифференциалы - все же не совсем одно и то же.

[Mihr]

А почему бы не писать $\Delta U = \frac{3}{2}\Delta (pV)$ ?

[gleensande]

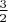
Для наибольшей точности и самопроверки можно сделать так: записать уравнения состояния для начального и конечного состояния и оттуда выразить $\nu RT$, соответственно дальше вычесть одно из другого, домножить на $\frac{3}{2}$ и получить нужную формулу для изменения внутренней энергии.

[DimaM]

gleensande в сообщении #1099769 писал(а):

оттуда выразить $\nu$RT

А зачем?

[gleensande]

Для понимания, откуда берется дельта объемов или давлений. Если понимание присутствует в должном виде, то, естественно, заморачиваться не следует.