Среди последовательных

чисел ровно
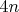
нечетных, следовательно сумма квадратов таких чисел делится на 4. А среди 5 последовательных чисел - или 2, или 3 нечетных, короче, сумма квадратов

последовательных чисел не может быть квадратом. Значит,

1)

Ищем среди 11 чисел:


Уравнение Пелля имеет решение

, значит имеет бесконечно много.
2)

- среди 7 чисел


нет решений по модулю 7
3)

- среди 6 чисел



- нет решений.
Только при
