Здравствуйте! У меня есть пару задач, с первой разобрался, вроде как (но не знаю -- правильно ли), а по второй мне кажется, что я неверно мыслю. Помогите, пожалуйста, разобраться!
1. Найти вероятность того, что симметричное случайное блуждание никогда не возвратится в ноль.
То есть требуется найти


Потому


То есть нужно найти


Верно ли это?
2. Пусть

-- симметричное блуждание на прямой. Используя принцип отражения, докажите, что:

Найдите распределение случайной величины

и найдите асимптотику

при

У меня тут только такая идея. Эта запись

означает вероятность того, что для любого
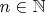
существует

такой, что

.
Правая часть

означает вероятность того ,что существует такой

, который меньше, чем

.
Для меня это все значит, что мы наугад выбрали точку на прямой. Вероятность того, что

будет больше

равна вероятности того, что

. То есть вероятности по

. Верно ли я понимаю?