Ограничения на псевдообратные матрицы

[Texture]

Добрый день!

Буду рад, если кто-нибудь подскажет или хотя бы даст вектор, куда копать по следующему вопросу:
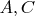
есть выражение $ABC$, где $A, B, C$ -- вектора соответствующих размеров, в результате произведения дающие квадратную матрицу. Матрицы $A, C$ не квадратные.

Требуется из знания выражения $D=ABC$ найти $B$.

Первой мыслью было использовать операцию взятия псевдообратнлой матрицы (зная, что это есть минимизация квадратов отклонений), то есть $B=A^{\dagger}DC^{\dagger}$. Как я понял, для того, чтобы матрица существовала, необходимо, чтобы существовало $(A^{\mathrm{T}}A)^{-1}$, то есть $\det(A^{\mathrm{T}}A)\neq 0$.

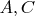
Пусть тогда есть матрица $D=\begin{bmatrix} d_{1} & d_{2} \\ d_{3} & d_{4}\end{bmatrix}$, $A=\begin{bmatrix} 0 \\ 1 \end{bmatrix}, C=\begin{bmatrix} 1 & 0 \end{bmatrix}$, тогда находя по вышеуказанным формулам получается $B=d_{3}$, подставляя обратно в $D=ABC$: $D=\begin{bmatrix} 0 & 0 \\ d_{3} & 0 \end{bmatrix}$, то есть вычеркиваются элементы из-за вида матриц $A, C$. Решал через матлаб, для такой $C$ он находит псевдообратную матрицу справа, если я правильно все понял.

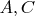
Вопрос заключается в том, какие должны быть ограничения на $A, C$ чтобы получить корректную $B$. Если я опять же правильно понимаю, то вопрос заключается в том, чтобы размеры подпространств совпадали с $D$ или не так?

Благодарю за любую помощь!

[iifat]

Texture в сообщении #1075438 писал(а):

$A, B, C$ -- вектора... Матрицы $A, C$ не квадратные

(Размахивает руками, отгоняя видение неквадратных векторов)
Насколько я помню, псевдообратная матрица определяется соотношением $AA^\dagger A=A$. Подставляя ваше $B$ в уравнение, получаем $ABC=AA^\dagger D C^\dagger C$. Как-то мне не очевидно, что это есть $D$.

-- 21.11.2015, 20:38 --

При заданных $A,C,D$ получаем систему линейных уравнений на компоненты $B$. Я б как-нить построил и попытался решить десяток примеров (разумеется, не руками и калькулятором).

-- 21.11.2015, 20:42 --

Не распишете конкретнее формы векторов? Что-то у меня не получается.

[Texture]

С описанием векторов-матриц получилось криво, да :(

iifat в сообщении #1075446 писал(а):

Насколько я помню, псевдообратная матрица определяется соотношением $AA^\dagger A=A$. Подставляя ваше $B$ в уравнение, получаем $ABC=AA^\dagger D C^\dagger C$. Как-то мне не очевидно, что это есть $D$.

По определению: $A^{\dagger}=(A^{T}A)^{-1}A^{T}$, подставляя, получим: $A^{\dagger}A=E_{n}$, это для левой обратной, с $C$ аналогично для правой.

iifat в сообщении #1075446 писал(а):

При заданных $A,C,D$ получаем систему линейных уравнений на компоненты $B$. Я б как-нить построил и попытался решить десяток примеров (разумеется, не руками и калькулятором).

-- 21.11.2015, 20:42 --

Не распишете конкретнее формы векторов? Что-то у меня не получается.

Система уравнений-то получается, но все опять же зависит от вида векторов. Вот и хочется узнать, когда получится правильный вариант, а когда -- нет.

Формы вектор для примера: $A=\begin{bmatrix} a_{1} \\ a_{2}\end{bmatrix}, B=\begin{bmatrix} b \end{bmatrix}, C=\begin{bmatrix} c_{1} & c_{2} \end{bmatrix}$. Их произведение: $D=ABC=\begin{bmatrix} d_{1} & d_{2} \\ d_{3} & d_{4} \end{bmatrix}$

Если взять $a_{1}=1, a_{2}=2, c_{1}=3, c_{2}=1, b=2$, но пока неизвестное, то $D=\begin{bmatrix} 6 & 2 \\ 12 & 4 \end{bmatrix}$, находя $A^{\dagger}DC^{\dagger}$ получается исходное $b=2$. Подставляя в $ABC$ получается исходное $D$.

[Slav-27]

Texture в сообщении #1075462 писал(а):

С описанием векторов-матриц получилось криво, да :(

Я так и не понял, кто у вас там вектор, а кто кто. $A$ - столбец, $B$ - чиселка, $C$ - строка? Если возможны ещё варианты, то скажите, какие.

[Texture]

Slav-27 в сообщении #1075474 писал(а):

Texture в сообщении #1075462 писал(а):

С описанием векторов-матриц получилось криво, да :(

Я так и не понял, кто у вас там вектор, а кто кто. $A$ - столбец, $B$ - чиселка, $C$ - строка? Если возможны ещё варианты, то скажите, какие.

На самом деле интересует больше конкретный вариант: $A$ -- столбец $R^{n}$, $B$ -- строка $R^{m}$ , $C$ -- матрица $R^{m\times n}$.

[Xaositect]

Texture в сообщении #1075475 писал(а):

На самом деле интересует больше конкретный вариант: $A$ -- столбец $R^{n}$, $B$ -- строка $R^{m}$ , $C$ -- матрица $R^{m\times n}$.

Не сходится. Если $A$ - столбец и $C$ - строка, то $B$ должна быть размера $1\times 1$

[Texture]

Xaositect в сообщении #1075480 писал(а):

Texture в сообщении #1075475 писал(а):

На самом деле интересует больше конкретный вариант: $A$ -- столбец $R^{n}$, $B$ -- строка $R^{m}$ , $C$ -- матрица $R^{m\times n}$.

Не сходится. Если $A$ - столбец и $C$ - строка, то $B$ должна быть размера $1\times 1$

Да, если $C$ -- строка, но интересует более общий случай, где, как я указал, $C$ -- матрица $R^{m\times n}$.

[Xaositect]

Ой, я перепутал $B$ и $C$.
Если $A$ - столбец, $B$ - строка и $C$ - матрица, то итоговая матрица $D = ABC$ будет ранга 1.
Матрица ранга 1 раскладывается в произведение столбца на строку $D = EF$ однозначно с точностью до преобразования $(E, F) \mapsto (k E, k^{-1} F)$. Одно такое разложение у нас есть - $D = A \cdot (BC)$

То есть, у нас все столбцы матрицы $D$ будут пропорциональны $A$, отсюда можно найти строку $BC$ и решить линейное уравнение для того, чтобы найти $B$.

[Texture]

Xaositect в сообщении #1075494 писал(а):

Ой, я перепутал $B$ и $C$.
Если $A$ - столбец, $B$ - строка и $C$ - матрица, то итоговая матрица $D = ABC$ будет ранга 1.
Матрица ранга 1 раскладывается в произведение столбца на строку $D = EF$ однозначно с точностью до преобразования $(E, F) \mapsto (k E, k^{-1} F)$. Одно такое разложение у нас есть - $D = A \cdot (BC)$

То есть, у нас все столбцы матрицы $D$ будут пропорциональны $A$, отсюда можно найти строку $BC$ и решить линейное уравнение для того, чтобы найти $B$.

Столбец на строку же даст матрицу, строка на столбец -- скаляр (при равенстве их размеров).

Но Вы заставили меня сомневаться, что я на всякий случай решил проверить :) Более наглядный пример:
$\begin{bmatrix}1 \\ 2 \\ 3 \\ 4 \end{bmatrix} \begin{bmatrix} 3 & 4 & 2 \end{bmatrix}\begin{bmatrix} 3 & 4 & 5 & 1 \\ 2 & 3 & 4 & 1 \\ 0 & -1 & 2 & 3 \end{bmatrix}=\begin{bmatrix} 17 & 22 & 35 & 13 \\ 34 & 44 & 70 & 26 \\ 51 & 66 & 105 & 39 \\ 68 & 88 & 140 & 52 \end{bmatrix}$

[Xaositect]

Texture в сообщении #1075500 писал(а):

Столбец на строку же даст матрицу

Ну да, матрицу ранга 1.

Texture в сообщении #1075500 писал(а):

Но Вы заставили меня сомневаться, что я на всякий случай решил проверить :) Более наглядный пример:
$\begin{bmatrix}1 \\ 2 \\ 3 \\ 4 \end{bmatrix} \begin{bmatrix} 3 & 4 & 2 \end{bmatrix}\begin{bmatrix} 3 & 4 & 5 & 1 \\ 2 & 3 & 4 & 1 \\ 0 & -1 & 2 & 3 \end{bmatrix}=\begin{bmatrix} 17 & 22 & 35 & 13 \\ 34 & 44 & 70 & 26 \\ 51 & 66 & 105 & 39 \\ 68 & 88 & 140 & 52 \end{bmatrix}$

Вот в этом примере все столбцы результата пропорциональны $\begin{bmatrix}1 \\ 2 \\ 3 \\ 4 \end{bmatrix}$. Отсюда мы можем сразу найти $BC = \begin{bmatrix} 17 & 22 & 35 & 13 \end{bmatrix}$, и это линейное уравнение относительно $B$.

[Texture]

Xaositect в сообщении #1075502 писал(а):

Texture в сообщении #1075500 писал(а):

Столбец на строку же даст матрицу

Ну да, матрицу ранга 1.

Texture в сообщении #1075500 писал(а):

Но Вы заставили меня сомневаться, что я на всякий случай решил проверить :) Более наглядный пример:
$\begin{bmatrix}1 \\ 2 \\ 3 \\ 4 \end{bmatrix} \begin{bmatrix} 3 & 4 & 2 \end{bmatrix}\begin{bmatrix} 3 & 4 & 5 & 1 \\ 2 & 3 & 4 & 1 \\ 0 & -1 & 2 & 3 \end{bmatrix}=\begin{bmatrix} 17 & 22 & 35 & 13 \\ 34 & 44 & 70 & 26 \\ 51 & 66 & 105 & 39 \\ 68 & 88 & 140 & 52 \end{bmatrix}$

Вот в этом примере все столбцы результата пропорциональны $\begin{bmatrix}1 \\ 2 \\ 3 \\ 4 \end{bmatrix}$. Отсюда мы можем сразу найти $BC = \begin{bmatrix} 17 & 22 & 35 & 13 \end{bmatrix}$, и это линейное уравнение относительно $B$.

Да, прошу прощения, сначала не совсем понял (точнее не вчитался), что Вы про ранг.

Хм, тогда у меня есть пара уточнений:
1) Строку из итоговой матрицы мы должны же взять ручками (никаким действием не вытащить?).
2) Брать строку и делить на соответствующее число из $A$?
3) После получения $BC=\begin{bmatrix} 17 & 22 & 35 & 13 \end{bmatrix}$ все равно использовать псевдообратную матрицу для $C$?

[Texture]

Texture в сообщении #1075504 писал(а):

1) Строку из итоговой матрицы мы должны же взять ручками (никаким действием не вытащить?).
2) Брать строку и делить на соответствующее число из $A$?
3) После получения $BC=\begin{bmatrix} 17 & 22 & 35 & 13 \end{bmatrix}$ все равно использовать псевдообратную матрицу для $C$?

С первыми двумя пунктами разобрался: домножаем $D$ слева на $\begin{bmatrix} 1 & 0 & \dots & 0 \end{bmatrix}$ и потом делим на $a_{1}$, если оно отлично от 1. Остается вопрос с последним. Для решения полученного уравнения опять придется использовать псевдообратную матрицу?

[Xaositect]

Texture в сообщении #1075577 писал(а):

С первыми двумя пунктами разобрался: домножаем $D$ слева на $\begin{bmatrix} 1 & 0 & \dots & 0 \end{bmatrix}$ и потом делим на $a_{1}$, если оно отлично от 1.

Если точнее, выбираем ненулевое $a_i$ и делим $i$-ю строку на него.

Texture в сообщении #1075577 писал(а):

Для решения полученного уравнения опять придется использовать псевдообратную матрицу?

Ну это как хотите. Можно псевдообратную, можно просто методом Гаусса.

[Texture]

Xaositect в сообщении #1075581 писал(а):

Если точнее, выбираем ненулевое $a_i$ и делим $i$-ю строку на него.

Да, именно это я имел в виду во втором уточнении, с этим понятно :)

Xaositect в сообщении #1075581 писал(а):

Ну это как хотите. Можно псевдообратную, можно просто методом Гаусса.

Мне, к сожалению, надо делать это конкретными математическими действиями, не методами, поэтому остается тогда псевдообратная.

Но мне все-таки больше требуется узнать ограничения, когда возможно решение такой системы. Пусть $D=\begin{bmatrix} 2 & 9 & 1 & 2 \\ 0 & 2 & 1 & -2 \\ 0 & 2 & 3 & 1 \\ 0 & 2 & 3 & 9 \end{bmatrix}$, $A=\begin{bmatrix} 0 \\ 0 \\ 0 \\ 1\end{bmatrix}$, $C=\begin{bmatrix} 1 & 2 & 3 & 4 \\ 3 & 9 & 2 & 3 \\ 2 & 3 & 1 & 0 \end{bmatrix}$, откуда получаем, что $BC=\begin{bmatrix} 0 & 2 & 3 & 9 \end{bmatrix}$, откуда с помощью псевдообращения в матлабе получаю
$B=\begin{bmatrix} 1.6206 & 0.6364 & -2.2213 \end{bmatrix}$. Теперь проверяем, подставляя в $ABC=\begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ -0.913 & 2.304 & 3.913 & 8.391 \end{bmatrix}$, что, очевидно, не совпадает с заданным $D$. Если я правильно понимаю, то должно же быть какое-то условие решения этого уравнения в духе того, что решение есть тогда и только тогда, когда $\det(D)=0$ (для обеспечения линейной-зависимости) и что-то должно быть с рангами $A, C$.. Прав ли я?

[Xaositect]

Texture в сообщении #1075620 писал(а):

Мне, к сожалению, надо делать это конкретными математическими действиями, не методами, поэтому остается тогда псевдообратная.

Откуда такие неестественные ограничения?

$D$ должна быть ранга $1$. Столбцы $D$ должны быть пропорциональны $A$, т.е. матрица $[D|A]$ тоже должна быть ранга 1. Система $BC = R$ полученная в процессе, должна иметь решение, т.е. удовлетворять условию теоремы Кронекера-Капелли.