Че-то никак не могу сообразить. Пытаюсь сочинить функцию

, скажем, непрерывную в окрестности нуля (скажем, на
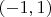
), которая бы удовлетворяла в этой окрестности, скажем, такому комплекту условий:
1. 
. В частности,

.
2. Но при этом, например,

.
(в педположении, что

и

соответственно)
На числах в условии 2 не настаиваю, возможно, потребуется какая-то несоизмеримость?...
То есть, задав функцию в какой-нибудь точке, по правилу 1 ее можно продлить на счетное число убегающих к нулю точек. И по правилу 2 тоже, но и точки будут другими. Можно ли непрерывно соединить эти точки так, чтобы условия сохранились для промежуточных точек?
Есть версия покопаться среди модулей непрерывности: слышал, что из них можно выносить целые константы, а нецелые вообще говоря нельзя.