Добрый день. У меня в моей работе (вообще говоря по теории автоматов) вознико некотрое понятие которое имеет алгебраическию интерпритацию. Пусть

-пруппа и

- ее подгруппа. Назовем

r-нормальной (этот термин я ввел сам) если существуют
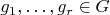
если

. Легко видеть что при

имеем,

, следовательно

. А в силу

получаем

для любого

. Что соответсвует нормальности

в

.
Я хотел бы узнать у алгебраистов, есть ли в алгебре что-нибудь подобное?