Пара мелких замечаний.
Во-первых, что можно построить линейкой (без делений) и циркулем, то можно построить и одним циркулем. Ссылки под рукой нет, было когда-то в Кванте. Можно поискать.
Во-вторых, обычно считается, что в четырёхугольнике

стороны

. Если так, то задача не всегда имеет решение: вот я беру
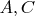
рядышком, а

на противоположном конце окружности.
Ну и тут принято приводить собственные попытки решения. Ну хоть признак описанного четырёхугольника приведите.