Интересные треугольники

[Vechnolos]

К сожалению, я с СТО и ОТО знаком лишь шапочно, поэтому наверняка сейчас "открою Америку". В свое оправдание скажу, что мне эти треугольники в научно-популярной литературе не попадались, поэтому встреча с ними меня так заинтересовала.

Я подметил вот такие треугольники:



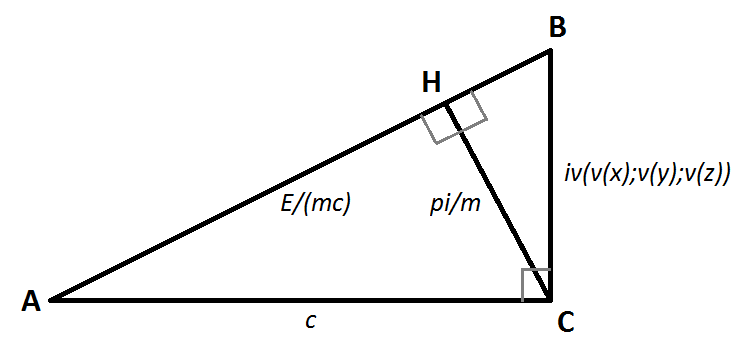
$\Delta ABC$ прямоугольный, его высота $CH$ делит треугольник еще на два прямоугольных треугольника: $\Delta AHC$ и $\Delta HBC$. Стороны треугольников равны:

$AC = c$, $CB = iv$, $AH = \frac{E}{mc}$ и $CH = \frac{pi}{m}$.

Забавно, но в этом треугольнике "сокрыты" четыре формулы:

1. $\Delta AHC$ прямоугольный, по теореме Пифагора имеем:

$(\frac{E}{mc})^2 + (\frac{pi}{m})^2 = c^2$

$\frac{E^2}{m^2 c^2} + \frac{p^2 i^2}{m^2} = c^2$

Умножим левую и правую часть на $m^2 c^2$ чтобы избавиться от знаменателя. Имеем:

$E^2 + i^2 p^2 c^2 = m^2 c^4$

Квадрат мнимой единицы равен $i^2 = -1$, а значит:

$E^2 - p^2 c^2 = (mc^2)^2$


2. $\cos BAC = \frac{AH}{AC} = \frac{AC}{AB}$

$\cos BAC = \frac{E}{m c^2} = \frac{c}{AB}$

Помня что $\Delta ABC$ прямоугольный, по теореме Пифагора находим:

$AB^2 = AC^2 + BC^2$

$AB^2 = c^2 + (iv)^2$

$AB = \sqrt{c^2 + i^2 v^2}$

А это значит:

$\cos BAC = \frac{E}{m c^2} = \frac{c}{\sqrt{c^2 + i^2 v^2}}$

$E = \frac{m c^3}{\sqrt{c^2 + i^2 v^2}}$

или более привычно (помня что $i^2 = -1$)

$E = m c^2 \gamma$, где $\gamma = \frac{1}{\sqrt{1 - \beta^2}}$, $\beta = \frac{v}{c}$


3. $\sin BAC = \frac{HC}{AC} = \frac{BC}{AB}$

$\sin BAC = \frac{p i}{m c} = \frac{i v}{\sqrt{c^2 + i^2 v^2}}$

$p = \frac{m v c}{\sqrt{c^2 + i^2 v^2}}$

или более привычно (помня что $i^2 = -1$)

$p = m v \gamma$, где $\gamma = \frac{1}{\sqrt{1 - \beta^2}}$, $\beta = \frac{v}{c}$


4. Легко заметить что $AB = AH + HB$, а с другой стороны что $AB^2 = AC^2 + BC^2$ (теорема Пифагора для прямоугольного треугольника $\Delta ABC$).

Нам неизвестно $HB$, но его можно вычислить из прямоугольного треугольника $\Delta HBC$ опять же по теореме Пифагора.

Не буду утомлять Вас математикой, результат подстановки данных в $AB^2 = (AH + HB)^2 =AC^2 + BC^2 $ и упрощения выражения таков:

$p = \frac{E v}{c^2}$


Забавно, как законы физики находят свое отражение в геометрии.

Ну и все это навивает на парочку вопросов:

1. Почему $c$ неизменна и постоянна? Хотя казалось бы $c$ не сильно отличается от $v$: все друг другу перпендикулярны $v_x \perp v_y \perp v_z \perp c$, все в равном положении.

2. Теоретически этот треугольник можно растянуть по $CB = iv$ так, чтобы $v >> c$, например, $v = 5 c$. Хотя такое действие неизбежно приведет к тому, что комплексная единица $i$ проникнет в формулу для $E$. Насколько это страшно?

3. Почему $c$ — это вещественное число, но $v i$ — мнимое? Треугольники можно перестроить таким образом, чтобы $v$ оказалась вещественным числом, но тогда неизбежно окажется что $c i$ — мнимое.

4. В физике нередко можно услышать гипотезу о мнимой массе $m i$. Но если попробовать перестроить этот треугольник так, чтобы масса оказалась мнимой, то все-равно либо $c$, либо $v$ сохранят у себя мнимую величину $i$ в добавок к мнимой величине $m i$. Так может решения надо искать в мнимой скорости, а не массе?

[arseniiv]

Vechnolos в сообщении #1056048 писал(а):

$CB = iv$

Как же построить отрезок такой длины?

-- Ср сен 23, 2015 21:13:30 --

Вообще, понятно, у древних греков были такие наклонности — все формулы превращать в соотношения между элементами каких-то фигур. Но их время уже давно прошло. На некоторые вещи лучше не натягивать такую интерпретацию. В частности, в СТО, у пространства Минковсеого геометрия неевклидова, так и не стоит его подпространства с неевклидовой геометрией (есть разные) описывать каким-то образом через евклидову.

Vechnolos в сообщении #1056048 писал(а):

1. Почему $c$ неизменна и постоянна? Хотя казалось бы $c$ не сильно отличается от $v$: все друг другу перпендикулярны $v_x \perp v_y \perp v_z \perp c$, все в равном положении.

Это в вашей интерпретации они «не сильно отличаются». Это, разумеется, не значит, что они не сильно отличаются вообще в соответствующей теории, откуда вы вытащили всего несколько деталей.

-- Ср сен 23, 2015 21:39:08 --

Vechnolos в сообщении #1056048 писал(а):

3. Почему $c$ — это вещественное число, но $v i$ — мнимое? Треугольники можно перестроить таким образом, чтобы $v$ оказалась вещественным числом, но тогда неизбежно окажется что $c i$ — мнимое.

Ну так вы сами сейчас на вопрос и ответили: потому что выбрали тот вариант, в котором всё так. Но вообще, конечно, см. выше: не зачем придумывать «псевдо»-евклидову геометрию с мнимыми длинами, когда есть псевдоевклидова, и с уже давно известным физическим наполнением.

Vechnolos в сообщении #1056048 писал(а):

4. В физике нередко можно услышать гипотезу о мнимой массе $m i$. Но если попробовать перестроить этот треугольник так, чтобы масса оказалась мнимой, то все-равно либо $c$, либо $v$ сохранят у себя мнимую величину $i$ в добавок к мнимой величине $m i$. Так может решения надо искать в мнимой скорости, а не массе?

Увы, нет. Мнимая масса появляется именно как мнимое число на том месте, на котором в некоторых уравнениях обычно находится вещественная обычная масса, и в том же контексте мнимая скорость бессмысленна. В любом случае, СТО — это один уровень, а КТП (насколько я знаю, такие вещи только там могут получаться) — вещь посложнее. Сначала надо разобраться с СТО.

-- Ср сен 23, 2015 21:48:42 --

(Оффтоп)

Кстати,

Vechnolos в сообщении #1056048 писал(а):

комплексная единица $i$

Комплексная единица — это, как ни странно, 1. Это единица этого поля в своём обычнейшем понимании. Число $i$ обычно называется мнимой единицей, и «единица» она в том смысле, что в $\mathbb C$ как евклидовом векторном пространстве над $\mathbb R$ она с обычной единицей составляет ортонормированный базис.

[Vechnolos]

arseniiv в сообщении #1056054 писал(а):

Vechnolos в сообщении #1056048 писал(а):

$CB = iv$

Как же построить отрезок такой длины?

Думаю, что это будет сложновато.

Пока относишься к мнимой единице $i$ как к обычной переменной, все прекрасно и красиво. Но стоит только попробовать что-то посчитать с ней, как на голову начинают ссыпаться парадокс за парадоксом.

arseniiv в сообщении #1056054 писал(а):

Вообще, понятно, у древних греков были такие наклонности — все формулы превращать в соотношения между элементами каких-то фигур. Но их время уже давно прошло. На некоторые вещи лучше не натягивать такую интерпретацию.

Я понимаю древних греков, такие совпадения производят и на меня сильное впечатление.

$AH^2 + HC^2 = AC^2$ похоже на $(\frac{E}{mc})^2 + (\frac{pi}{m})^2 = c^2$

$\cos BAC = \frac{AH}{AC} = \frac{AC}{AB} = \frac{E}{m c^2} = \frac{c}{\sqrt{c^2 + i^2 v^2}}$

$\sin BAC = \frac{HC}{AC} = \frac{BC}{AB} = \frac{p i}{m c} = \frac{i v}{\sqrt{c^2 + i^2 v^2}}$

$AB^2 = (AH + HB)^2 =AC^2 + BC^2 $ приведет к $p = \frac{E v}{c^2}$

Тут уж хочешь не хочешь, начинает складываться мнение что это «ж-ж-ж» неспроста.

[arseniiv]

Vechnolos в сообщении #1056062 писал(а):

Но стоит только попробовать что-то посчитать с ней, как на голову начинают ссыпаться парадокс за парадоксом.

Да не, считать-то с ней как раз нормально…

Vechnolos в сообщении #1056062 писал(а):

Тут уж хочешь не хочешь, начинает складываться мнение что это «ж-ж-ж» неспроста.

Ну так подойдите уже к предмету правильно — начните изучать СТО. И понимание будет ясным. А спорадические совпадения ещё ни о чём не говорят.

[Sicker]

Vechnolos
Гуглить псевдоевклидова геометрия.

-- 23.09.2015, 20:05 --

Да, вы верно подметили геометрическую интерпретацию, по на уровне мнимых длин в евклидовой геометрии.Фишка в том, что мы делаем эти мнимые длины вещественными и меняем знак в теореме Пифагора.(может быть сами справитесь?)

[arseniiv]

А, чего это я тут советую читать СТО, а ничего не привёл. Vechnolos, Тейлора, Уилера «Физика пространства-времени» читали? Это возможное начало, просто чтобы распутать в какой-то степени.

-- Ср сен 23, 2015 22:09:01 --

Sicker в сообщении #1056066 писал(а):

Фишка в том, что мы делаем эти мнимые длины вещественными и меняем знак в теореме Пифагора.

Боюсь, педагогического содержания здесь ноль. Я бы честно не понял, или понял обязательно неправильно.

[Sicker]

arseniiv
Я просто объясняю измышления ТС в правильном ключе.
Раньше было мнимое время в СТО.

[Утундрий]

Vechnolos скорее всего чей-то клон.

[Vechnolos]

Sicker в сообщении #1056066 писал(а):

Да, вы верно подметили геометрическую интерпретацию, по на уровне мнимых длин в евклидовой геометрии.Фишка в том, что мы делаем эти мнимые длины вещественными и меняем знак в теореме Пифагора.(может быть сами справитесь?)

Что-то типа такого?

$\sqrt{c^2 + i^2 v^2} = \sqrt{c^2 - v^2}$

arseniiv в сообщении #1056065 писал(а):

Vechnolos в сообщении #1056062 писал(а):

Тут уж хочешь не хочешь, начинает складываться мнение что это «ж-ж-ж» неспроста.

Ну так подойдите уже к предмету правильно — начните изучать СТО. И понимание будет ясным. А спорадические совпадения ещё ни о чём не говорят.

Про изучение СТО Вы безусловно правы, но так ли случайно это совпадение? Я никак не могу отделаться от мысли, что за такой изящной аналогией что-то стоит.

arseniiv в сообщении #1056067 писал(а):

А, чего это я тут советую читать СТО, а ничего не привёл. Vechnolos, Тейлора, Уилера «Физика пространства-времени» читали? Это возможное начало, просто чтобы распутать в какой-то степени.

За наводку спасибо! Сегодня вечером изучу. Надеюсь там не слишком сложное изложение материала? А то, боюсь, у меня могут возникнуть сложности. Мое знание материала, как Вы наверное успели заметить, на уровне научно-популярных книг и статей.

[Sicker]

Vechnolos в сообщении #1056075 писал(а):

Что-то типа такого?

Не совсем... Там между пространством и временем только.

[Vechnolos]

Утундрий в сообщении #1056073 писал(а):

Vechnolos скорее всего чей-то клон.

Я как-то один раз спрашивал совета в «Помогите решить / разобраться (Ф)» на похожую тематику, но я не помню пароля от логина. Тогда я вел себя адекватно и меня не банили, если Вы про это.

Sicker в сообщении #1056076 писал(а):

Vechnolos в сообщении #1056075 писал(а):

Что-то типа такого?

Не совсем... Там между пространством и временем только.

Прочитал в Вики про мнимое время. Весьма интересная идея, надо будет узнать по подробнее. Правда в этих треугольниках времени вообще нет.

[profrotter]

Тема перемещена из форума «Физика» в форум «Помогите решить / разобраться (Ф)»
Причина переноса: в более подходящий раздел.

[arseniiv]

Sicker в сообщении #1056071 писал(а):

Раньше было мнимое время в СТО.

Раньше — да. Но потом люди поняли, что раз пространство-время не евклидово, а комплексные числа только добавляют возможной путаницы (как так, одна компонента 4-вектора всегда мнимая, а другие всегда действительны?), то нечего. И стали пользоваться псевдометрикой явно, а не глядя через штору.

Sicker в сообщении #1056076 писал(а):

Не совсем... Там между пространством и временем только.

Я же говорил, что непонятно «объяснили». Если бы можно было так в двух словах, это бы давно и делали.

Vechnolos в сообщении #1056075 писал(а):

Про изучение СТО Вы безусловно правы, но так ли случайно это совпадение? Я никак не могу отделаться от мысли, что за такой изящной аналогией что-то стоит.

Да, стоит: $a^2 = -(ai)^2$. Просто потому что $\pm i$ — это квадратный корень из $-1$, а смена знака — это умножение на $-1$. И всё; аналогия проста как пробка.

Vechnolos в сообщении #1056075 писал(а):

Надеюсь там не слишком сложное изложение материала?

Не, там, наоборот, не слишком много сведений растянуто. Так что за вечер прочитать надеяться не стоит.

[Vechnolos]

arseniiv в сообщении #1056085 писал(а):

Vechnolos в сообщении #1056075 писал(а):

Надеюсь там не слишком сложное изложение материала?

Не, там, наоборот, не слишком много сведений растянуто. Так что за вечер прочитать надеяться не стоит.

То что такие книги за раз не читаются, меня не страшит. Наоборот, хорошо когда изложение подробное.