А Ваши рис. теории соответствуют?

[romanov59]

Частный случай есть частный случай не надо его забывать. Он приведен в учебнике Савельева Курс общей физики в 5 томах издание 4 1998г. стр 202 - 203 первого тома Механика. Цитата: В силу принципа относительности системы $ K $ и $ K' $ совершенно равноправны. Единственное формальное различие их заключается в том, что отсчитанная в системе $ K $ иксовая координата начала $ O' $ системы $ K' $ изменяется по закону
$ x_{O '} $ = $ V_ O t $ , в то время как отсчитанная в системе $ K' $ иксовая координата начала $ O $ системы $ K $ изменяется по закону
$ x' _O = - V_O t' $
Это различие вызвано тем, что направления осей $ x $ и $ x' $ мы выбрали одинаковыми, а системы $ K $ и $ K' $ движутся относительно друг друга в противоположных напрвлениях. Поэтому проекция относительной скорости на ось $ x $ системы $ K $ равна $ V_O $ , а на ось $ x' $ системы $ K' $ равна $- V_ O $ .
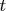
Как видим хороший частный случай из которого разные координаты и расстояния в силу различия $ t $ и $ t' $ выдаются за одно расстояние. Ведь $ O $ - $O' $ равно $ O'$ - $ O $ . $ x_{ O'} $= расстояние $ O $ - $O' $, а $ x' _O $= расстояние $ O' $ - $ O $ .
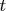
Все сначала и ладом - это для новой теории. Бездумно копировать рисунок из одной теории в другую не надо. Для определения расстояния между началами есть одна скорость и разные времена. Если за время $ t $ попали в т. $ O' $, а за время $ t' $ не попали обратно, то сделайте соответствующую поправку в рисунке. Кстати в системе $ K $ есть только начало системы $ K' $ и наоборот.

[Pphantom]

Тема перемещена из форума «Дискуссионные темы (Ф)» в форум «Пургаторий (Ф)»
Причина переноса: помимо собственных "достоинств", это возобновление темы из Карантина.

romanov59 - предупреждение, см.выше.