Назовем две функции подобными, если они совпадают или отличаются только коэффициентами. Например, подобны

и

,

и

. Очевидно, отношение подобия рефлексивно, симметрично и транзитивно, т.е. любое множество функций распадается на классы подобных друг другу функций.
Множество всех элементарных функций континуально (например, одних только прямых

континуум, т.к. каждое действительное значение

образует свою прямую), но во множестве всех элементарных функций счетное число классов подобия. В символических вычислениях мы можем не различать подобные функции, а в численных расчетах вместо коэффициентов подставляются рациональные числа. Поэтому с классом всех элементарных функций можно работать.
Меня интересует такое множество хороших замкнутых по уравнениям функций, в котором счетное число классов подобия. С ним тоже можно будет работать.
Итак, в нашем гипотетическом множестве:
1. Счетное число классов подобия.
2. Каждый класс подобия закодирован фразой конечного алфавита (как фраза

кодирует класс подобия логарифмических функций).
3. Существует алгоритм, который по классу подобия функции возвращает класс подобия ее производной (для элементарных функций такой алгоритм есть, он сводится к таблице производных и правилам дифференцирования).
"Взять" функцию - найти символическую запись ее класса подобия. Для уравнения

такая запись, например,

и

. Далее можно дифференцировать эти

и вообще делать с ними что угодно.
Другой вопрос - а как по уравнению найти запись функции, выражающей его решение? В самом общем виде такая проблема, увы, алгоритмически неразрешима. Что не исключает существования алгоритмов для достаточно широкого класса уравнений. В частности, алгоритма, который по уравнению

выдает символическую запись функции
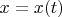
.