Хотелось бы конечно что-нибудь чисто геометрическое, без тригонометрии, обозначений для углов и пр. Вначале увлёкся выкладками и перестал об этом думать. Но вот сейчас, кажется, придумал.
Мы считаем, что точки
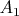
и

различны. Из условия имеем

, так что

и

.
Пусть

--- середина отрезка
![$[A_1A_5]$ $[A_1A_5]$](https://dxdy-01.korotkov.co.uk/f/0/7/d/07d188d87dac56185c98f694db12a1b882.png)
. Предположим, что точка
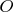
не лежит на плоскости

. Тогда существует единственная плоскость

, содержащая точки

,

и
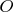
.
Из равенств

следует, что либо

, либо
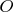
не лежит на прямой

. Но

, ибо

, так что

и мы можем говорить о треугольнике

. Этот треугольник равнобедренный и отрезок
![$[OD]$ $[OD]$](https://dxdy-02.korotkov.co.uk/f/5/b/c/5bcc58b743aab8d192604216f5532e3b82.png)
является его медианой. Значит, он также является высотой этого треугольника и

. Кроме того,

и так как плоскость

содержит две прямые, перпендикулярные

, то она сама перпендикулярна

.
Пусть

--- середина отрезка
![$[A_2A_4]$ $[A_2A_4]$](https://dxdy-04.korotkov.co.uk/f/b/1/6/b168c15c0d50e3a0477018704899e1ac82.png)
. Так как

, то либо точка
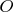
совпадает с точкой

, либо
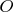
не принадлежит прямой

. А поскольку

, то имеет место последнее. Таким образом, мы имеем право говорить о треугольнике

. Этот треугольник равнобедренный и так как отрезок
![$[OE]$ $[OE]$](https://dxdy-02.korotkov.co.uk/f/d/0/0/d00c67fbf92f3d7e395c02c386efb81582.png)
есть его медиана, то он же является и высотой, так что

. Аналогично

,

--- равнобедренный треугольник, его медиана
![$[A_3E]$ $[A_3E]$](https://dxdy-01.korotkov.co.uk/f/8/f/c/8fc3383b8dafc6b38ec696e4ca88347782.png)
является также и высотой и прямая

перпендикулярна плоскости

.
Если
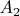
не лежит на прямой

, то

--- треугольник. Из равенств

и

следует, что

--- тоже треугольник и эти треугольники равны по трём сторонам. Значит,

, так что треугольники

и

равны по двум сторонам и углу между ними. Из равенства же этих треугольников вытекает

A_5E|$.
Если же точка
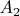
лежит на прямой

, то из равенств расстояний

,

опять следует, что $|A_1E| = |A_5E|.
Итак,

в обоих случаях. Значит, либо

, либо

из рассмотрения равнобедренного треугольника

. В обоих случаях точка

принадлежит плоскости

. Следовательно, плоскость

совпадает с

и прямые

,

параллельны (либо совпадают) как перпендикулярные одной и той же плоскости.
Предположив, что эти прямые совпадают, из

сразу получим

, в то время как справедливо обратное. Значит, прямые не совпадают, а просто параллельны.
Симметричные рассуждения дают параллельность прямых

и

, а также прямых

и

.
Из этого, в свою очередь, следует, что плоскости

и

параллельны или совпадают.
Пусть эти плоскости не совпадают. Из того, что прямая

лежит в плоскости, параллельной плоскости

и перпендикулярна

следует, что она параллельна прямой

. Причём обе прямые,

и

лежат в плоскости

. Так как

, то либо

|A_3E|, либо

. Однако из параллельностей и перпендикулярностей

, так что

и

--- параллелограмм. Из равенств

и

следует, что точка
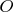
лежит на пересечении диагоналей этого параллелограмма. Значит, она является серединой отрезка
![$[A_3A_6]$ $[A_3A_6]$](https://dxdy-02.korotkov.co.uk/f/1/0/7/1070bb60b7721a2d40930a1f7f5e12cc82.png)
.
Теперь

, так что точка

является серединой отрезка
![$[A_3O]$ $[A_3O]$](https://dxdy-04.korotkov.co.uk/f/3/6/9/36928a2d9962c9d33cab2fd21945a2bd82.png)
. Получаем, что диагонали параллелограмма пересекаются более чем в одной точке. Противоречие.
Ближайшее допущение, которое мы делали --- это предположение о несовпадении плоскостей

и

. Из полученного противоречия имеем равенство этих плоскостей, то есть одну и ту же плоскость. Прямые

и

лежат в этой плоскости и в плоскости

, а так как

не совпадает с плоскостью

, то, значит, указанные прямые равны и совпадают с линией пересечения плоскостей. Но тогда

и

. Как и ранее, из того, что отрезки
![$[A_1A_5]$ $[A_1A_5]$](https://dxdy-01.korotkov.co.uk/f/0/7/d/07d188d87dac56185c98f694db12a1b882.png)
и
![$[A_2A_4]$ $[A_2A_4]$](https://dxdy-04.korotkov.co.uk/f/b/1/6/b168c15c0d50e3a0477018704899e1ac82.png)
параллельны и равны по длине, следует, что либо

, либо

. Во втором случае

, однако из

следует, что точки

и

лежат между точками

и

и

.
Значит,

и

--- прямоугольник. Если предположить, что точка

лежит от прямой

по ту же сторону, что и точка

, то получим

, чего не может быть. Аналогично

и

лежат по разные стороны от прямой

и

. Однако

и

. А поскольку

, то

, чего не может быть.
Противоречие мы теперь получили с предположением, что точка
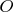
не лежит в плоскости

. Значит, она там лежит. Из равенств

выводим, что точка
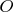
совпадает с центром треугольника

. Далее, из

сразу следует, что

. Отсюда получаем

. Таким образом, точка

лежит на отрезке
![$[OA_6]$ $[OA_6]$](https://dxdy-04.korotkov.co.uk/f/7/d/2/7d29ce245151126ad7e08d8b7a97db0d82.png)
,

лежит на прямой

и попадает в плоскость

. Принадлежность этой же плоскости точек
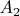
и

доказывается аналогично.



