Ничего не понимаю. Давайте разберем пример какой-нибудь стратегии для

что ли. Допустим первый игрок загадал 4. Опишите действия второго по какой-нибудь из стратегий.
Цитата:
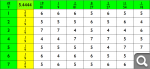
Выбираем первую стратегию - {6, 5, 7, 4, 5, 6, 5}
Находим максимум в векторе-стратегии - это 7 на позиции 3. Значит выбираем 3.
Получаем ответ "больше", теперь стратегии с номерами с 1 до 3 включительно недоступны - {6, 5, 7, 4, 5, 6, 5}.
А в оставшейся части максимум 6 на позиции 6, значит 6 и выбираем.
Получаем ответ "меньше", теперь доступны только стратегии номер 4 и 5 - {6, 5, 7, 4, 5, 6, 5}.
В оставшейся части максимум (5) на пятой позиции, соответственно 5 и называем(из-за позиции).
Получаем ответ "меньше" - {6, 5, 7, 4, 5, 6, 5}.
Остаётся только стратегия 4, её и выбираем, выигрывая 4 очка.
Цитата:
Альтернатива - выбираем седьмую стратегию - {5, 4, 6, 5, 7, 5, 6}.
Находим максимум в векторе-стратегии - это 7 на позиции 5. Значит выбираем 5.
Получаем ответ "меньше", теперь стратегии с номерами с 5 до 7 включительно недоступны - {5, 4, 6, 5, 7, 5, 6}.
В оставшейся части максимум (6) на третьей позиции, соответственно называем 3.
Получаем ответ "больше", теперь доступна только стратегия 4 - {5, 4, 6, 5, 7, 5, 6}.
Выбираем стратегию 4 и получаем 5 очков.



