Но измерение производится когда колесо уже раскручено и вращается с постоянной скоростью, сил упругости, которые являются реакцией на деформацию треугольника
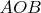
, уже нет
так они уже передвинули концы стержня друг от друга. от того что они исчезли те обратно не придвинутся
Без наличия упругой деформации в точке крепления спиц собственное расстояние между точками

измениться не может, иначе колдовство какое-то получается
Следовательно треугольник
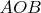
должен иметь собственные размеры неизменными, т.к. он жесткий (отрезки

и

по условию эксперимента жестко закреплены в точке

).
нет конечно, в неинерциальной системе отсчета геометрические соотношения не подчиняются правилам эвклидовой геометрии, сумма углов треугольника не равна 180. а "собственные размеры" у вращающегося треугольника вы можете определить только в такой системе отсчета. если вы сохранили две стороны и угол между ними то третья сторона увеличивается, если сохранили три стороны и три угла то стороны перестанут быть прямыми, спицы изогнутся
Мне не нужны собственные размеры всего треугольника
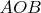
, а только отрезка

. Любая неподвижная часть целого (при отсутствии упругих деформаций) должна иметь собственные размеры. Отрезок

неподвижен в системе отсчета измеряемого отрезка. Если вы имеете ввиду то, что он вращается вокруг своей середины (или вокруг одного из своих концов), то это вращение не меняет его длины, т.к. у точек нет продольных скоростей.
Единственное место, где может остаться деформация
да не должна оставаться деформация. деформация понадобилась бы чтобы вернуть собственное расстояние обратно, чтобы сохранить его увеличенным она не нужна
Странное утверждение. Упругая деформация возникает при изменении собственных размеров, и исчезает при возвращении собственных размеров. Т.е. упругая деформация есть только тогда, когда есть относительное удлинение/сжатие. Если никаких деформаций нет, то собственные размеры жесткого тела неизменны.
-- 11.02.2015, 12:10 --Мешает жесткое закрепление спиц в центре колеса.
Жёсткое закрепление спиц в центре ничему не мешает: расстояния в центре не увеличиваются, и потому никакие напряжения не возникают. Расстояния увеличиваются вдали от центра.
Вообще, я однажды уже писал: колесо релятивистского курвиметра должно быть устроено так, чтобы его радиус не изменялся. Тогда оно будет правильно измерять длину кривой.
Вопрос о том, что будет происходить с реальным колесом в процессе раскрутки и последующего вращения с постоянной скоростью, который Вы пытаетесь здесь решать, относится не к физике, а к другой дисциплине — сопротивлению материалов.
Причем здесь сопротивление материалов? По-вашему от материала курвиметра зависит совпадут или нет результаты измерения отрезка в разных ИСО?