Решил в этой теме привести в систему сведения о тензорном произведении линейных пространств, которые обсуждались в теме
http://dxdy.ru/topic61294.htmlИ, вообще-то, по уму, понятия прямой суммы, произведения и тензорного произведения надо определять в категорных терминах, через универсальные объекты. Это будет наиболее логично, красиво и правильно.
Определение тензорного произведенияПусть

-- линейные пространства, и пусть

-- билинейное отображение. Если оно универсально в следующем смысле: для любого билинейного отображения

существует единственное линейное отображение

такое, что

, то

называется
тензорным произведением пространств

и

![$$
\xymatrix{
X\times Y \ar[r]^-\varphi \ar[rd]_-\psi & Z \ar@{-->}[d]^-f \\
& W}
$$ $$
\xymatrix{
X\times Y \ar[r]^-\varphi \ar[rd]_-\psi & Z \ar@{-->}[d]^-f \\
& W}
$$](https://dxdy-03.korotkov.co.uk/f/2/e/4/2e44096712c8b3eb72e3b3155e5bd55382.png)
(на этой диаграмме пунктирная стрелка означает существование и единственность отображения)
Значение билинейного отображения

обозначается

и называется тензорным произведением элементов

.
Единственность тензорного произведенияТензорное произведение пространств

,

единственно с точностью до изоморфизма в следующем смысле:
Если

,

-- два тензорных произведения, и

-- соответствующие им универсальные билинейные отображения

, то существует единственный линейный изоморфизм

такой, что

![$$
\xymatrix{
& & Z_1 \ar@{-->}[dd]^-f \\
X\times Y \ar[rru]^-{\varphi_1} \ar[rrd]_-{\varphi_2} & & \\
& & Z_2
}
$$ $$
\xymatrix{
& & Z_1 \ar@{-->}[dd]^-f \\
X\times Y \ar[rru]^-{\varphi_1} \ar[rrd]_-{\varphi_2} & & \\
& & Z_2
}
$$](https://dxdy-02.korotkov.co.uk/f/d/2/e/d2eb005efb394d6b3f13977bba1f347682.png)
Доказательство. Согласно определению тензорного произведения существует единственное линейное отображение

такое, что

, и существует единственное линейное отображение

такое, что

![$$
\xymatrix{
& & Z_1 \ar@/^7pt/@{-->}[dd]^-f \\
X\times Y \ar[rru]^-{\varphi_1} \ar[rrd]_-{\varphi_2} & & \\
& & Z_2\ar@/^7pt/@{-->}[uu]^-g
}
$$ $$
\xymatrix{
& & Z_1 \ar@/^7pt/@{-->}[dd]^-f \\
X\times Y \ar[rru]^-{\varphi_1} \ar[rrd]_-{\varphi_2} & & \\
& & Z_2\ar@/^7pt/@{-->}[uu]^-g
}
$$](https://dxdy-01.korotkov.co.uk/f/8/e/c/8ec1ab8c16f8fab15752178e5e8dfe9782.png)
Из этой коммутативной диаграммы получаем, что для линейного отображения

выполнено

. По определению тензорного произведения существует ровно одно линейное отображение

с таким свойством. Но для тождественного отображения

равенство

выполняется. Следовательно

. Аналогично получаем

. Следовательно

,

-- взаимно обратные линейные отображения, т.е.

-- линейный изоморфизм.
Существование тензорного произведенияТеперь надо конструктивно построить хотя бы одно пространство

и билинейное отображение

, удовлетворяющие определению тензорного произведения.
Рассмотрим свободное линейное пространство порожденное декартовым произведением

. То есть множество всех формальных линейных комбинаций вида

, где

-- скаляры,

,

,

. Обозначим это пространство буквой

. Можно также сказать, что

является базисом Гамеля пространства

. Более формально

можно определить как множество всех числовых функций, заданных на множестве

и отличных от нуля только в конечном числе точек.
В

рассмотрим линейное подпространство

, порожденное всеми элементами вида

где

пробегают

,

пробегают

,

пробегает поле скаляров.
Фактор-пространство

и будет искомым тензорным произведением. Его элементами являются классы смежности по подпространству

, т.е. множества вида

, где

. Сложение и умножение на скаляры происходит по представителям:

,

. Нулевой элемент в

-- само подпространство

.
Обозначим через
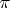
каноническую проекцию

. Она сопоставляет элементу

содержащий его класс эквивалентности

. Заметим, что
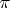
является линейным отображением.
Определим билинейное отображение

следующим образом

. Проверим билинейность (она возникает из-за специального устройства подпространства

):

Аналогично

и т.д.
Проверим универсальность отображения

. Пусть

-- билинейное отображение. Так как

-- свободное пространство, порожденное множеством

, то существует (причем только одно) линейное отображение

такое, что

для любых

.
Заметим, что на подпространстве

отображение

обращается в нуль. Действительно, т.к.
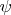
билинейно, то


и т.д. А такие элементы порождают

.
Т.к.

, то

для некоторого линейного отображения

. Для любых

имеем

. Таким образом,

. Единственность такого линейного отображения очевидна, т.к. элементы

порождают

.
Таким образом, пространство

и билинейное отображение

удовлетворяют определению тензорного произведения.
Критерий тензорного произведенияСформулируем необходимое и достаточное условие для того, чтобы линейное пространство

вместе с билинейные отображением

удовлетворяло определению тензорного произведения:
Лемма. Пусть  -- билинейное отображение. Обозначим
-- билинейное отображение. Обозначим  . Пространство
. Пространство  вместе с отображением
вместе с отображением  является тензорным произведением
является тензорным произведением  и
и  тогда и только тогда, когда выполняются следуюшие два условия:
тогда и только тогда, когда выполняются следуюшие два условия:
1) элементы  порождают
порождают  ;
;
2) если  -- конечная линейно независимая система векторов в
-- конечная линейно независимая система векторов в  ,
,  -- конечная линейно независимая система векторов в
-- конечная линейно независимая система векторов в  , то
, то  -- линейно независимая система векторов в
-- линейно независимая система векторов в  .
.Доказательство. Сначала докажем необходимость. Пусть

,

-- соответствующее билинейное отображение. Для обоснования условий 1) и 2) будем использовать только свойство универсальности отображения

.
Предположим, что не выполняется условие 1), т.е. подпространство

, порожденное элементами

, является собственным подпространством пространства

. Тогда кроме тождественного отображения

уравнению

удовлетворяет также любое отображение

, совпадающее на

с

, но во всем пространстве отличное от

. Такое отображение можно получить в виде

, где

-- ненулевой линейный функционал на

, равный нулю на

, а

-- любой ненулевой вектор в

. Следовательно свойство универсальности нарушается в части единственности.
Докажем условие 2) Пусть вектора

линейно независимы в

, а вектора

линейное независимы в

. Тогда существуют линейные функционалы

такие, что

для всех

, и линейные функционалы

такие, что

для всех

.
Обозначим буквой

свободное линейное пространство, порожденное множеством всех пар

, т.е. множество всех формальных линейных комбинаций таких пар. Рассмотрим следующее билинейное отображение

:

Нетрудно видеть, что

для всех

,

.
Согласно определению тензорного произведения существует единственное линейное отображение

такое, что

для всех
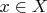
,

. В частности,

. Так как система векторов

линейно независима в

(она является базисом этого пространства), то система векторов

обязана быть линейно независимой в

.
Докажем теперь достаточность условий леммы. Пусть линейное пространство

вместе с билинейным отображением

,

удовлетворяет условиям 1),2). Покажем, что тогда

вместе с

является тензорным произведением

и

.
Пусть

--
какое-либо тензорное произведение пространств

, и

,

-- соответствующее универсальное билинейное отображение. По определению тензорного произведения существует единственное линейное отображение

, такое, что

![$$
\xymatrix{
& & Z_1 \ar@{-->}[dd]^-f \\
X\times Y \ar[rru]^-{\varphi_1} \ar[rrd]_-{\varphi} & & \\
& & Z
}
$$ $$
\xymatrix{
& & Z_1 \ar@{-->}[dd]^-f \\
X\times Y \ar[rru]^-{\varphi_1} \ar[rrd]_-{\varphi} & & \\
& & Z
}
$$](https://dxdy-01.korotkov.co.uk/f/0/9/6/096ba0feb5561bb4103595c8ff90530e82.png)
Покажем, что

-- линейный измоморфизм между

и

. Отсюда будет следовать, что

вместе с

также является тензорным произведением

и

.
Так как

, для любых
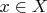
,

, и по условию 1) эти элементы порождают

, то

Пусть

для некоторого

. По доказанному

можно представить в виде

-- конечная сумма. Пусть

-- базис линейной оболочки векторов

,

-- базис линейной оболочки векторов

. Тогда

можно переписать в виде

.
Имеем

По условию 2) система векторов

линейно независима в

. Отсюда все коэффициенты

. Значит,

. Значит,

.
Лемма доказана.
Другие реализации тензорного произведенияОпределение 2.Рассмотрим пространство

билинейных функционалов

. Тензорным произведением пространств

называется линейная оболочка элементов

Пусть

-- векторные пространства. И

-- пространство билинейных функций

. Тензорным произведением элементов
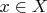
и

(обозначается

) называется отображение

. Это отображение является элементом

. Т.е. это линейная функция на

Линейная оболочка множества всевозможных

называется тензорным произведением пространств

.
Проверим, что определение 2 удовлетворяет условиям леммы. Условие 1) выполняется по определению. Проверим условие 2) Пусть

-- конечная линейно независимая система векторов в

,

-- конечная линейно независимая система векторов в

. Предположим, что

. По определению это означает, что

для любых функционалов

,

. Выбирая функционалы

и

так, чтобы

,

, получим, что все коэффициента

. Значит, система векторов

линейно независима.
Проверка для определения 3 точно такая же. Условие 1) -- по определению. Если

, то по определению это значит, что для любой билинейной функции

выполнено

. В частности это выполняется для любых функционалов вида

, где

,

. А этот случай мы уже рассмотрели.