Проверьте, пожалуйста, правильность доказательства теоремы:
Теорема (об ошибке полиномиальной интерполяции).Пусть

— функция из
![${{C}^{n+1}}\left[ a,b \right]$ ${{C}^{n+1}}\left[ a,b \right]$](https://dxdy-03.korotkov.co.uk/f/2/a/5/2a50041c4be8b60d25e5b3e651364f5182.png)
и пусть

— полином степени

, который интерполирует функцию

в

отличной друг от друга точке
![${{x}_{0}},{{x}_{1}},\ldots ,{{x}_{n}}\in \left[ a,b \right]$ ${{x}_{0}},{{x}_{1}},\ldots ,{{x}_{n}}\in \left[ a,b \right]$](https://dxdy-02.korotkov.co.uk/f/9/b/5/9b52ae439d15f2b0019daef4bdffccdc82.png)
. Пусть

— так же функция из
![${{C}^{n+1}}\left[ a,b \right]$ ${{C}^{n+1}}\left[ a,b \right]$](https://dxdy-03.korotkov.co.uk/f/2/a/5/2a50041c4be8b60d25e5b3e651364f5182.png)
, которая в указанных точках интерполяции (и только в них на отрезке
![$\left[ a,b \right]$ $\left[ a,b \right]$](https://dxdy-02.korotkov.co.uk/f/9/f/b/9fb84e4297cfbcdc1186ca6b114843db82.png)
) обращается в нуль, а её производная

отлична от нуля всюду на отрезке
![$\left[ a,b \right]$ $\left[ a,b \right]$](https://dxdy-02.korotkov.co.uk/f/9/f/b/9fb84e4297cfbcdc1186ca6b114843db82.png)
. Тогда для любой точки
![$x\in \left[ a,b \right]$ $x\in \left[ a,b \right]$](https://dxdy-03.korotkov.co.uk/f/a/6/8/a68f77562e529d8ae77fa109d2d0d4da82.png)
существует такая точка
![$\xi \in \left[ a,b \right]$ $\xi \in \left[ a,b \right]$](https://dxdy-02.korotkov.co.uk/f/d/a/5/da5a1df655a463c475e9d6909213dd2e82.png)
, что:
![$$\[f\left( x \right)-p\left( x \right)=\frac{{{f}^{\left( n+1 \right)}}\left( \xi \right)}{{{g}^{\left( n+1 \right)}}\left( \xi \right)}g\left( x \right)\]$$ $$\[f\left( x \right)-p\left( x \right)=\frac{{{f}^{\left( n+1 \right)}}\left( \xi \right)}{{{g}^{\left( n+1 \right)}}\left( \xi \right)}g\left( x \right)\]$$](https://dxdy-01.korotkov.co.uk/f/c/0/a/c0a465617d70641795734381b173b96282.png) Доказательство.
Доказательство.Если точка

является одной из точек интерполяции

, то правая и левая части равенства обращаются в нуль, и утверждение теоремы истинно. Теперь предположим, что

,

. Введём функцию

Функция
![$\varphi \left( t \right)\in {{C}^{n+1}}\left[ a,b \right]$ $\varphi \left( t \right)\in {{C}^{n+1}}\left[ a,b \right]$](https://dxdy-02.korotkov.co.uk/f/9/4/f/94fdbf8e8bbdd43817cb95be1379881382.png)
, а так же обращается в нуль в

отличных друг от друга точках: в точках интерполяции и в точке

. По теореме Ролля производная

обращается в нуль в

различной точке. Кроме того, производная
![${\varphi }'\left( t \right)\in {{C}^{n}}\left[ a,b \right]$ ${\varphi }'\left( t \right)\in {{C}^{n}}\left[ a,b \right]$](https://dxdy-02.korotkov.co.uk/f/9/c/6/9c67f3512d401b0bf961382258df3f2a82.png)
, следовательно, так же удовлетворяет теореме Ролля, и вторая производная

обращается в нуль в

различных точках. Продолжая таким образом получим, что на отрезке
![$\left[ a,b \right]$ $\left[ a,b \right]$](https://dxdy-02.korotkov.co.uk/f/9/f/b/9fb84e4297cfbcdc1186ca6b114843db82.png)
существует такая точка, назовём её
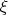
, в которой производная

обращается в нуль. Выражение для производной:

Но

— полином степени

, поэтому

, и:

Отсюда окончательно получаем:
