Какие вообще интересные вещи я увижу?
Ну раз модератор настаивает, перепосчу свои примитивные выкладки, как раз под желаемый, как мне кажется, уровень восприятия.
Замечаю, что изложение упрощенное, краями наверное и даже не совсем аккуратное, поэтому еще раз: под текущий уровень, это скорее "на пальцах", хотя что то более существенное, чем картинки воронок из науч-попа. Далее уже Торн и товарищи.
Вкратце без погружения в СТО, то на пальцах можно объяснить подход ОТО применительно к Ньютонизму следующим образом:
Т.е. смотрим на гравитацию глазами Ньютонизма так как её объясняет ОТО.
Если поместить наблюдателя в ускоряющуюся ракету (т.е. смотреть на мир глазами НЕинерциальной системы отсчета), то он найдет основной закон механики

"поломанным". На тела не действует никакая сила, а они почему то ускоряются в направлении куда направлены движки. А чтобы тело покоилось - к нему надо приложить силу. Выправить уравнение можно двумя путями: а) предположить что тела действует некая фиктивная сила. Здесь придется обратить внимание на то, что размер этой силы подстраивается под массу тела, чтобы обеспечить всем телам одинаковое ускорение:

. Но именно так ведет себя гравитационное поле. Таким образом приходим к выводу, что неИСО можно легко описывать если предположить что в нём действует фиктивное гравиполе.
Но можно пойти другим путем - предположить что гравиполе и есть неИСО! НЕТ силы, но само уравнение для описания движения в неИСО без введения силы должно всё правильно описывать.
Тогда имеем другую форму уравнения:

, где g по сути постоянный член, "сносящий" все координаты со временем.
Нетрудно заметить, что сферически гравитирующему телу невозможно сопоставить неИСО, т.к. надо "ускоряться во всех направлениях". Но это физически невозможно... если только само пространство не будет кривым, чтобы "падать" со всеми телами в нём на планету со всех направлений "обжимаясь и деформируясь". Можно упрощенно сказать, что вариация "сносящего координаты со временем" фактора g по пространству и есть кривизна пространства-времени.
Любопытно рассмотреть гравиполе бесконечной пластины в каждом из полупространств которое пластина делит всё пространство оно эквивалентно неИСО ускоренной ракеты, без криволинейностей, поэтому просто рассуждать опять таки в рамках Ньютонизма.
С точки зрения неИСО наблюдателя находящегося на поверхности пластины все тела над пластиной на него синхронно и с одинаковым ускорением падают, т.е. если на тело не действуют силы, движутся по кривым - параболам. Если подкинуть мяч под углом, он снова и снова будет по параболе падать на пластину, отскакивая.
Но перенесемся в ИСО одного из таких свободно падающих тел и картинка станет радикально другой - нет никакой гравитации, все свободно подвешенные тела летят по прямым, а это снизу ускоряясь взлетает какая то значит вот пластина. Мяч летит по прямой, но пластина снова и снова его догоняет в своём ускоренном движении и снова и снова подталкивает вверх, отскакивая же мяч всё время летит по прямой.
Таким образом мы видим, что то что было кривыми в неИСО пластины в другой системе отсчета есть прямолинейное движение по инерции и тут даже возникает догадка, что эта иная система отсчета и есть самая настоящая ИСО.
Таким образом неИСО пластины наблюдает как бы свободно падающую ИСО, перекраивая наблюдения в формуле через g-фактор

, можно говорить что само пространство падает на пластину со всеми телами в нём, двигающимися по инерции.
Так, ну это Ньютонистический срез, а вот в релятивизме уже всё сильно осложнено тем, что неИСО становится намного богаче на доп-поправки, нежели один коэффициентик.
Итак, понятно, чтобы осмыслить бесконечную гравитирующую пластину надо суметь построить наблюдения из неИСО, в чём, кстати, зачастую СТО обвиняют что она этого не может, а в ОТО собственно (и это действительно так исторически) слово "Общая" относится к способности описывать процессы в неИСО.
Тем не менее можно воспользоваться сразу же напрашивающейся "техникой мгновенно-сопутствующих ИСО", чтобы попытаться себе понять что же в неИСО происходит на некотором уровне и какие гравитационные эффекты оно подразумевает.
Одним из важнейших и практически коренных свойств СТО является относительность одновременности. Если одна ИСО движется относительно другой, то события происходящие в ней в другой происходят в другом порядке.
Конкретно - если поезд в нашей ИСО едет слева-направо, то одновременные события в ИСО поезда в нашей ИСО происходят сперва те которые левее, причем чем левее, тем раньше, а потом уже те которые правее, причём тем более потом, чем они правее.
Нетрудно догадаться, что если в неподвижной ИСО события еще одновременны, а в движущейся уже неодновременны, то эта неодновременность "накапливается" именно при смене скорости, т.к. во время действия ускорения.
Тогда, взяв разгоняющуюся ракету и каждому моменту собственного времени сопоставив преобразования Лоренца мгновенно-сопутствующую ИСО (МСИСО) и сложив их картинки вдоль одной линии времени мы придём к некой "координатной сетке линейно ускоряющейся релятивистской неИСО".
Что в ней будет наблюдаться?
Рассинхронизация времени нарастает, причём в пространстве спереди носа ракеты часы начинают спешить и тем дальше, чем дальше до них расстояние. Позади ракеты часы начинают оставать и тем больше, чем больше до них расстояние. Т.е. процесс динамический - если переди покоился стержень, то пока мы набираем к нему скорость (как и в Ньютонизме снос координат), то задний конец в этом процессе обгоняет передний, т.е. стержень естественно-динамически сокращает свою длину. Более того, мы знаем что все изначально неподвижные стержни заранее расставленные вдоль всего пространства должны в каждой из МСИСО сократится одинаково, значит стержни на очень далёких расстояниях вперед падают очень быстро, быстрее скорости света, потому что часы в них спешат очень и очень быстро. Нетрудно догадаться, что в линейном гравиполе расстояние по высоте тесно связано с понятием "гравипотенциала", поэтому и говорится, что время в областях с высоким гравипотенциалом течет быстрее времени в областях с низким гравипотенциалом.
Обратим теперь еще более пристальное внимание назад в пространстве, за корму ракеты. Там время часов замедляется, вплоть до некоторого рубежа где скорость течения времени совсем останавливается. Более того, сравнивая МСИСО мы найдем, что за этой точкой время течет вспять! Стержни которые должны были бы удалятся, на самом деле приближаются! Ибо помним, что все стержни в каждой МСИСО сокращены одинаково.
Получается всё пространство спереди падает на какой то рубеж позади, а пространство позади этого рубежа падает опять таки на него же наизнанку с той стороны!
Визуализация прилагается:
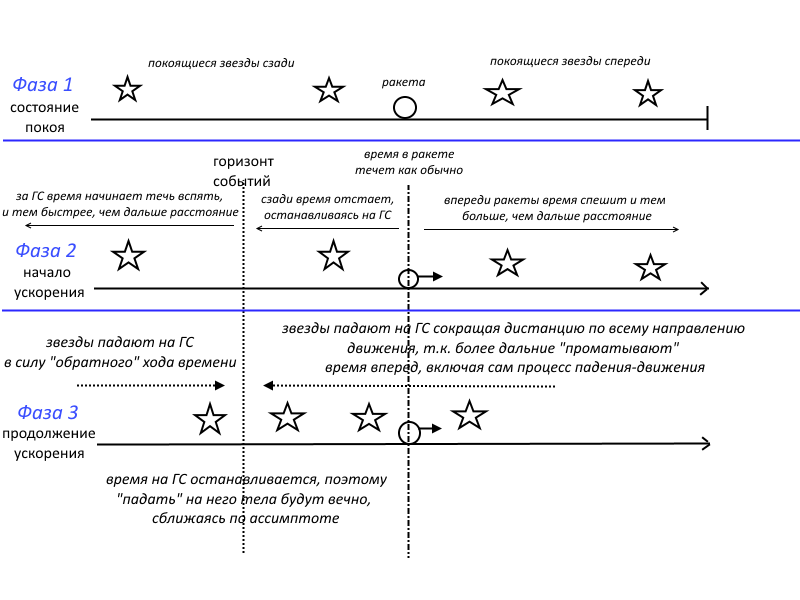
Итак, в неИСО ракеты мы наблюдаем самый настоящий горизонт событий, причём он в принципе существует в любой неИСО и обладает следующими свойствами:
а) время всех процессов при приближении к нему замирает, вплоть до полной остановки
б) время процессов за ним как бы проматывается назад, но здесь сразу замечу, в ОТО так не говорят и такого вывода не делают, а обрывают покрытие координатной сеткой т.н. "удаленного наблюдателя" на этом месте.
в) в связи с тем что время останавливается невозможно взаимодействие с за-ГС-ной областью (вот что хранит нас от теоретического взаимодействия с прошлым), любой сигнал, включая свет, замрёт на месте при подлете к ГС
Отсюда интересные выводы. Если с космонавт ракеты кинет в ГС яблоко, оно в его неИСО будет вечно падать на него и никогда не достигнет за-ГС-ной области.
Но в СО такого _свободно падающего_ яблока, которая, как мы выяснили выше, есть банальная ИСО, никакого гравиполя нет вообще, нет никакого ГС, можно свободно обмениваться сигналами с за-ГС-ной областью, пролетая мимо того места, которое в неИСО ракеты было ГС яблоко _вообще ничего не заметит_. Нет никакого гравиполя и никаких его эффектов.
Но как тогда объяснить то, что объекты за ГС не могут обмениваться с ракетой сигналами?
Дело в том, что кинематика релятивистской ускоряющейся ракеты такова, что пока она по ассимптоте ускоряется к скорости света в ИСО яблока существует расстояние начиная с которого испущенный даже световой сигнал никогда ракету не догонит, пока она продолжает ускорятся. Они опять таки сближаются по ассимптоте, но никогда не сравняются.
Таким образом _действительно_ есть область за которой обмен сигналами с ракетой невозможен. Но в ИСО яблока она объясняется просто тем, что ракета постоянно улетает ускоряясь к скорости света, в то время как в неИСО ракеты оно объясняется существованием горизонта событий, т.е. в сущности, существованием гравиполя.
Поэтому, если подытожить:
а) зависший над ГС наблюдатель подобен той ракете (и действительно чтобы оставаться на месте ему надо непрерывно держать двигатели включенными = ускоряться вверх в гравиполе, иначе он начнёт падать). Но он так называемый "удаленный наблюдатель".
б) сбросив яблоко такой удаленный наблюдатель будет вечно наблюдать его ассимптотическое падение на ГС, моментов времени когда яблоко окажется под ГС в его системе отсчета просто никогда не будет. это разрыв систем отсчета.
в) падающее яблоко падая вообще не заметит никакого ГС, зато в поле реальной сферически-симметричной ЧД заметит приливные силы, но это уже второй вопрос. третий вопрос - что оно заметит при попадании в сингулярность, всё спрессовывается в точку с делением на ноль.
г) если с яблока в момент пролета мимо ГС испустить луч света в направлении ракеты, то свет вечно замрет в этой месте. причём с точки зрения ракеты он просто вморожен в одну точку с нулевым течением времени. с точки зрения же самого луча (или наблюдателя к нему близкого) он вечно летит сквозь падающее на него сверху пространство к вечно улетающей от него ракете, не сокращая и не увеличивая дистанцию. можно сказать что вся вселенная снаружи от него куда то "удаляется" со скоростью света, и его собственной скорости света хватает лишь для того чтобы стоять на месте.
Таким образом ГС ЧД это нифига не вторая космическая, это вообще разрыв мозга, координатных сеток и пространства и времени. Приводится иногда такая аналогия - что смотря на глобус с одной стороны ты видишь только часть его координатной сетки и чтобы увидеть другую, нужно обойти его с другой стороны. Но при этом в ОТО ты теряешь возможность вернуться обратно.
Как то так.
|
i |
Было бы полезно при "перепосчивании" еще и формулы нормально оформить... Исправил. |



