Таким образом, вы согласились, что раскрутка колеса не имеет значения. Имеет значение только текущее состояние колеса, когда оно уже раскручено. Теперь рассмотрите движущийся треугольник
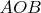
(т.к. перемычек на колесе нет, и на размеры этого треугольника не влияет состояние других спиц). Напряжений, изгибающих спицы

и

нет - следовательно меняться собственной длине отрезка

причин нет. А учитывая, что точки

и

этого треугольника неподвижны - отрезок

должен иметь собственную длину, которая равна

.
все ровно наоборот, в процессе раскручивания силы упругости в спицах увеличивают собственное расстояние между их кончиками. этого можно было бы ИЗБЕЖАТЬ соединив пару спиц жесткой перемычкой, противостоящей этим силам упругости в спицах. а коли мы этого не делаем то собственное расстояние увеличивается и становится больше

вы все ровно наоборот понимаете. это чтобы сохранить собственное расстояние нужно изогнуть спицы, а не чтобы изменить
Вы пишете: "В процессе раскручивания силы упругости в спицах увеличивают собственное расстояние между их кончиками". Но измерение производится когда колесо уже раскручено и вращается с постоянной скоростью, сил упругости, которые являются реакцией на деформацию треугольника
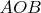
, уже нет. Следовательно треугольник
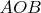
должен иметь собственные размеры неизменными, т.к. он жесткий (отрезки

и

по условию эксперимента жестко закреплены в точке

).
Единственное место, где может остаться деформация, - это точка

. Влияние деформаций в точке

на собственную длину отрезка

можно учесть, если рассмотреть эту точку "под микроскопом". Как это можно учесть я уже отвечал на комментарий
xinef, привожу ответ еще раз:
"... центр колеса не математическая точка и должен иметь хоть и малый, но размер, поэтому Лоренцево сокращение его частей может влиять на величину отрезка

. Это легко учесть. Пусть центр колеса является сколь угодно малым, но сплошным диском. Т.к. этот диск имеет сколь угодно малый размер, то линейная скорость точек его обода сколь угодно мала по сравнению со скоростью поступательного движения этого диска как целого (в ИСО измеряемого отрезка). Это означает, что релятивистских эффектов, связанных с вращением этого маленького диска нет, т.е. преобладают релятивистские эффекты, связанные с его движением как целого. При движении же этого диска как целого все его продольные размеры сокращаются, значит сокращается и бесконечно малый участок его обода, связывающий две соседние спицы, которые в данный момент соприкасаются с измеряемым отрезком. Таким образом, Лоренцево сокращение центра курвиметра может привести только к уменьшению отрезка

, соприкасающегося с измеряемым отрезком. Но этот эффект только усугубляет противоречие, т.к. длина измеряемого отрезка в ИСО, где он неподвижен, становится не равной, а большей, чем

сегментов колеса, в то время как в ИСО неподвижного центра курвиметра длина измеряемого отрезка
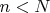
".
-- 04.02.2015, 10:56 --В том-то и дело, что обода у колеса курвиметра нет.
Тогда, стало быть, ничто не помешает увеличению расстояния между спицами в собственной системе отсчёта.
Мешает жесткое закрепление спиц в центре колеса. Как это может повлиять на собственную длину отрезка

я написал в своем предыдущем комментарии для
rustot.