Здравствуйте. Помогите, пожалуйста, разобраться.
Допустим есть матрица:

где

- вещественные числа. Надо сосчитать собственные значения и вектора.
Собственные значения:

.
А вот с векторами я что-то туплю.
Например, для

:
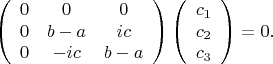
Как я понимаю, то

произвольно, а вот, что с

и

? Ведь для того, чтобы они нашлись необходимо еще одно условие

. И вот это меня ставит в ступор. Что-то важное я забыл из линейки, помоги, пожалуйста.