Ответ, разумеется, находится на первых страницах любого учебника по электротехники. Главное изучать электротехнику последовательно.
Специально открыл учебник — на первых страницах идет речь вообще про электрическое поле.
Прежде чем замахиваться на законы коммутации, подумайте над более простой задачей: есть источник напряжения и мы его закоротили. Теперь между его выводами с одной стороны напряжение не равно нулю, а с другой равно.
У меня есть только такое объяснение: можно взять условное сопротивление
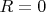
, тогда

, а

— неопределенность, может быть любым числом. Но это какое-то сомнительное объяснение, может быть есть другое?