информационная сеть и теория относительности

[telik]

Пусть частица передает свою квантовую информацию в сеть Вселенной по формуле:
$K m=\frac{I}{t}$

где m- масса частицы, $\frac{I}{t}$- количество переданной информации в квантовую сеть Вселенной за единицу времени (кубит/с), К -коэффициент пропорциональности в формуле.

Рассмотрим движение частицы в инерциальной системе отсчета


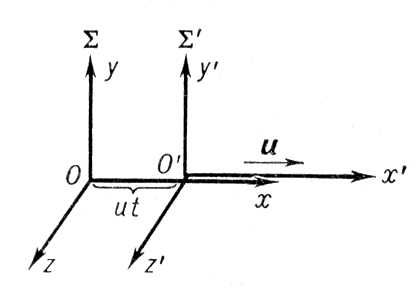
Относительно неподвижной системы отсчета, количество информации будет:
$K m_{0}=\frac{I_{0}}{t_{0}}$.

В системе отсчета, где частица движется появляется дополнительный информационный поток от квантовой сети Вселенной:
$I=I_{0}+\Delta I$

Или $K m t=K m_{0}t_{0}+\Delta I$

Ясно что дополнительный информ.поток является функцией следующих величин:

$$\Delta I = f (m, V, t) = K m t \alpha (V)$$

Уравнение баланса информации имеет вид:

$K m t=K m_{0}t_{0}+K m t \alpha (V)

Или по другому сокращая коэффициент К:

$m t (1-\alpha (V))= m_{0}t_{0}

Используем закон сохранения импульса для двух шаров с одинаковыми массами , пусть один из шаров движется навстречу другому и происходит касательное столкновение , в результате оба шара получают поперечные импульсы.

$py=py^{|}$

Или

$$m \frac{y}{t}= m^{|} \frac{y^{|}}{t^{|}}$$

Так как $y=y^{|}$
Отсюда получаем

$$\frac{m}{t}= \frac{m^{|}}{t^{|}}$$

Зная этот факт, и подставляя в уравнении информационного баланса , находим выражения:

$m_{0}=m \sqrt {1-\alpha(V)}$

$t_{0}=t \sqrt {1-\alpha(V)}$

Далее используя свойство однородности и изотропности пространства , определяем альфу функцию как четную:

$\alpha(V)=\alpha(-V)=k V^{2}$

Отсюда получается кинематический ( по сути информационный) эффект замедления времени:

$t_{0}=t \sqrt {1-k V^{2}}$

Ясно теперь, почему существует предельная скорость, потому что скорость обработки информации в квантовой сети Вселенной является конечной величиной

[_Z_]

telik в сообщении #941137 писал(а):

сеть Вселенной

Это типа вселенского интернета что ли?

[telik]

_Z_ в сообщении #941161 писал(а):

telik в сообщении #941137 писал(а):

сеть Вселенной

Это типа вселенского интернета что ли?

Можете называть это интернетом Вселенной или гигантским квантовым компьютером. По моему все частицы материи обмениваются квантовой информацией с пространством ( информационная сеть в виде квантовой запутанности )

[Touol]

telik в сообщении #941137 писал(а):

свою квантовую информацию в сеть Вселенной

А что такое квантовая информация частицы???
Уважаемый telik.Ваши сообщения меня уже несколько раздражают. Конечно, квантовая информация играет большую роль, но ваши формулы и высказывания не согласуются с научным понятием информации. Например из
Ю.Л. Климонтович Энтропия и информация открытых систем
S-информация:
$I(x)=\int f(X)\ln f(X) dX$
Как она связана с $K m=\frac{I}{t}$???

[telik]

Touol в сообщении #941189 писал(а):

telik в сообщении #941137 писал(а):

свою квантовую информацию в сеть Вселенной

А что такое квантовая информация частицы???
S-информация:
$I(x)=\int f(X)\ln f(X) dX$
Как она связана с $K m=\frac{I}{t}$???

Существуют предел вычисления Бремерманнаhttps://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B5%D0%B4%D0%B5%D0%BB_%D0%91%D1%80%D0%B5%D0%BC%D0%B5%D1%80%D0%BC%D0%B0%D0%BD%D0%BD%D0%B0 . Оттуда взята эта формула

[spyphy]

telik в сообщении #941137 писал(а):

Отсюда получаем

$$\frac{m}{t}= \frac{m^{|}}{t^{|}}$$

Зная этот факт, и подставляя в уравнении информационного баланса , находим выражения:

$m_{0}=m \sqrt {1-\alpha(V)}$

можете расписать этот переход?

[Touol]

Цитата:

Преде́л Бремерма́нна, названный в честь Ханса-Йоахима Бремермана enru — максимальная скорость вычислений автономной системы в материальной вселенной. Выводится из эйнштейновской эквивалентности массы-энергии и соотношений неопределённости Гейзенберга и составляет c2/h ≈ 1,36 × 1050 бит в секунду на килограмм.

Интересно . Но в честь чего

telik в сообщении #941137 писал(а):

Пусть частица передает свою квантовую информацию в сеть Вселенной по формуле:
$K m=\frac{I}{t}$

Почему вдруг максимальная скорость вычислений превращается в частица передает свою квантовую информацию?

[telik]

spyphy в сообщении #941212 писал(а):

telik в сообщении #941137 писал(а):

Отсюда получаем

$$\frac{m}{t}= \frac{m^{|}}{t^{|}}$$

Зная этот факт, и подставляя в уравнении информационного баланса , находим выражения:

$m_{0}=m \sqrt {1-\alpha(V)}$

можете расписать этот переход?

$m t (1-\alpha (V))= m_{0}t_{0}

$$\frac{m}{t}= \frac{m_{0}}{t_{0}}$$

или

$$t= \frac{mt_{0}}{m_{0}}$$

$$m \frac{mt_{0}}{m_{0}} ((1-\alpha (V))= m_{0}t_{0}$$

$m_{0}^{2}=m^{2} (1-\alpha(V))$

-- 06.12.2014, 19:59 --

Touol в сообщении #941215 писал(а):

Цитата:

Преде́л Бремерма́нна, названный в честь Ханса-Йоахима Бремермана enru — максимальная скорость вычислений автономной системы в материальной вселенной. Выводится из эйнштейновской эквивалентности массы-энергии и соотношений неопределённости Гейзенберга и составляет c2/h ≈ 1,36 × 1050 бит в секунду на килограмм.

Интересно . Но в честь чего

telik в сообщении #941137 писал(а):

Пусть частица передает свою квантовую информацию в сеть Вселенной по формуле:
$K m=\frac{I}{t}$

Почему вдруг максимальная скорость вычислений превращается в частица передает свою квантовую информацию?

Потому формула универсальна. Она связывает массу с понятием информации. Все частицы обладают массой, следовательно по данной формуле передают информацию с определенным трафиком:

$ m c^{2}=h\frac{\Delta I}{\Delta t}$

[Touol]

telik в сообщении #941218 писал(а):

Потому формула универсальна. Она связывает массу с понятием информации.

Связывает, но формула не универсальна. Она применима только предел для какого-то максимального производительного компьютера. (жаль вывод не нашел .)

telik в сообщении #941218 писал(а):

Все частицы обладают массой, следовательно по данной формуле передают информацию

Вообще не обязательно чтоб частицы обладали такой информацией. Необязательно, чтоб они ее обрабатывали. Тем более необязательно, чтоб они ее куда-то передавали!

[telik]

Touol в сообщении #941226 писал(а):

Вообще не обязательно чтоб частицы обладали такой информацией. Необязательно, чтоб они ее обрабатывали. Тем более необязательно, чтоб они ее куда-то передавали!

Есть такой принцип , он появился недавно в работах Хокинга , Бекенштейна, тХофта, Малденсаны и т.д. Называется голографический принцип. Все свойства трехмерного мира можно записать на поверхности. Бекенштейн получил результат, что энтропия в системе не может превышать:

$S<\frac{Mc R}{h}$

-- 06.12.2014, 20:24 --

Собственно можно выразить массу частицы через производство энтропии квантовой запутанности:

$m= \frac{h}{c^{2}} \frac{\Delta S}{\Delta t}$

Тогда получается что инертность - это квантовая запутанность между частицей и физическим вакуумом (пространство).

[Touol]

telik в сообщении #941230 писал(а):

Бекенштейн получил результат, что энтропия в системе не может превышать:

$S<\frac{Mc R}{h}$

что такое $R$?

telik в сообщении #941230 писал(а):

производство энтропии квантовой запутанности

Где определение энтропии квантовой запутанности?

[spyphy]

А что там по цифрам получается? Если в формулу данные подставить, то постоянную скорости света получим?

[warlock66613]

Munin в сообщении #920112 писал(а):

Физики шутят писал(а):

<...отрезано важное, см. в сообщении Munin...>
В данной работе нами был рассмотрен кристалл с гексагональной решеткой. Как известно, при абсолютном нуле температуры в, системе происходит вымораживание всех степеней свободы, то есть прекращаются полностью все внутренние колебания. Однако для электрона, движущегося по боровской орбите, это обстоятельство не имеет места. Каждый такой электрон, согласно Эддингтону, обладает $1/\alpha$ степенями свободы, где $\alpha$ – введенная Зоммерфельдом постоянная тонкой структуры. Поскольку рассматриваемый нами кристалл состоит также из протонов, которые по теории Дирака можно рассматривать как дырки в электронном газе, то к $1/\alpha$ степеням свободы электрона следует добавить столько же степеней свободы протона. Таким образом, чтобы достичь абсолютного нуля температуры, мы должны отнять у нашей нейтральной системы (наш кристалл должен быть электрически нейтральным), состоящей из одного электрона и протона (в расчете на один нейтрон), $- (2/\alpha- 1)$ степеней свободы (Freiheitsgrade). Единицу мы вычли, чтобы не учитывать вращательного движения.
Следовательно, для температуры абсолютного нуля находим $T_0 = - (2/\alpha-1)$ градусов (Grade). Подставив сюда $T_0 = -273,$ находим, что $\alpha= 1/137.$ Это значение в пределах ошибок находится в замечательном согласии с ранее известным значением. Легко показать, что этот результат не зависит от выбора структуры кристаллической решетки.
<...отрезано важное, см. в сообщении Munin...>

[Cos(x-pi/2)]

warlock66613


Вспомнилась вот такая статьюшка в нешуточном журнале серьёзных времён (1974 г): Формула зависимости между математическими и физическими константами. И фамилия у автора, как сейчас сказали бы, знаковая - Лоренц. :))

В той статье и примечание примечательное:
<< Первое равенство в формуле (3), полученное на основе «непонятной формулы Эйлера», редакция оставляет на совести автора. >>

[npduel]

telik в сообщении #941137 писал(а):

Пусть частица передает свою квантовую информацию в сеть Вселенной...

В Вашу частицу вмонтирован радиопередатчик? Частица карманных размеров или перевозится на автомобиле?