Обобщение Фибоначчи по простому модулю и циклы де Брёйна

[fractalon]

Доброе время! Возникла такая вот гипотеза (которую проверил для чисел до $10^5$):
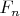
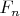
для любого простого числа $p$ существует константа $c$ такая, что последовательность, определённая как $F_0=0$, $F_1=1$, $F_n=cF_{n-2}+cF_{n-1}$, если её элементы взять по модулю $p$ (то есть взять остатки от деления $F_n$ на $p$) образует почти полный цикл де Брёйна, то есть первые $p^2$ остатков от деления членов $F_n$ на $p$ содержат среди себя все возможные двухэлементные непрерывные подпоследовательности (кроме $0 0$, иначе последовательность зациклилась бы).

Например, для $p=5$ таким значением будет $c=2$ и, соответственно, удовлетворять условию будут числа вида $F_n=2F_{n-2}+2F_{n-1}$. Значениями последовательности по модулю $p$ в этом случае будут:

$0, 1, 2, 1, 1, 4,$
$0, 3, 1, 3, 3, 2,$
$0, 4, 3, 4, 4, 1,$
$0, 2, 4, 2, 2, 3,$
$0, 1, 2, 1, 1, 4,$
$0, 3, 1, 3, 3, 2$
...и так далее...

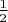
Ну, да это ладно, прелесть в другом. Прелесть в том, что примерно для половины чисел $p$ минимальным значением $c$ является первообразный корень (слово "примерно" тут, конечно же, означает, что доля таких $p$, видимо, стремится к $\frac{1}{2}$). Экспериментально пока установлено, что для чисел, меньших $100000$, доля таких составляет $0.498645$.

Хотелось бы узнать мнение знатоков, есть ли в математике уже такие результаты, или, может быть, тут вообще всё тривиально и я чего-то туплю?

Пока нет времени исследовать всё подробно, вот я и решил осведомиться, не изобретаю ли велосипед.

[Null]

1. Вам важнее то, что $-c$ - первообразный корень.
2. Можно переформулировать задачу так:
У одного из многочленов вида $x^2-cx-c$ корень - примитивный элемент поля $F_{p^2}$(порождающий элемент мультипликативной группы).
Ну или у многочлена $x^p+x^{p-1}+1$ один из корней примитивный элемент.

получается интересный вывод: произведение всех неприводимых многочленов вида $x^2-cx-c$ и $x+2$ равно $x^p+x^{p-1}+1$ (по модулю $p$)

[vicvolf]

Null в сообщении #939450 писал(а):

получается интересный вывод: произведение всех неприводимых многочленов вида $x^2-cx-c$ и $x+2$ равно $x^p+x^{p-1}+1$ (по модулю $p$)

Это не задача, а гипотеза. Задачей является ее доказать.

[maxal]

fractalon в сообщении #938067 писал(а):

Доброе время! Возникла такая вот гипотеза (которую проверил для чисел до $10^5$):
для любого простого числа $p$ существует константа $c$ такая, что последовательность, определённая как $F_0=0$, $F_1=1$, $F_n=cF_{n-2}+cF_{n-1}$, если её элементы взять по модулю $p$ (то есть взять остатки от деления $F_n$ на $p$) образует почти полный цикл де Брёйна, то есть первые $p^2$ остатков от деления членов $F_n$ на $p$ содержат среди себя все возможные двухэлементные непрерывные подпоследовательности (кроме $0 0$, иначе последовательность зациклилась бы).

Другими словами, существует такое $c$, что многочлен $x^2-cx-c$ над $\mathrm{GF}(p)$ является примитивным.

[Null]

maxal, я тоже самое написал. Просто бывают другие примитивные многочлены. Еще бы найти какой-нибудь критерий примитивности.

vicvolf, то что вы выделили не гипотеза, а доказанное утверждение.

Можно доказывать что один из многочленов $x^2+x+c$ - примитивный.

[Null]

Вроде как удалось доказать что если $\frac{\varphi(p+1)}{2}+\varphi(p-1)>\frac{p-1}{2}$, то решения есть, но к сожалению так выполняется не всегда.
Доказательство:
Работаем в поле $F_{p^2}$, р -нечетное, простое.
1. Если $x^{p-1}$ -порядка $p+1$ и $x^{p+1}$ -порядка $p-1$, то $x$ - порядка $p^2-1$.
Действительно: Если $x$ -порядка m, то $m|p^2-1$, $m=kl$, где $k|p+1$, $l|p-1$. Но тогда
$x^{(p-1)k}=1$, откуда $p+1|k$ и $x^{(p+1)l}=1$, откуда $p-1|l$,а значит $p^2-1|kl$.

2. $y^p$ -операция сопряжения. Откуда
$t(x)=x^p+x\in F_p$
$n(x)=x^{p+1}\in F_p$
$b(x)=x^{p-1}+x^{1-p}+2\in F_p$. т.к.$b(x)=\frac{t^2(x)}{n(x)}$

3.Множество значений $x^{p-1},x \in F^*_{p^2}$ - циклическая группа по умножению. В ней $\varphi(p+1)$ порождающих элементов. Пусть они образуют множество $S$
Если $x\in S$, то $\frac{1}{x}\in S$
$ S\cap F_p=\varnothing$ т.к. иначе $x^{(p-1)(p-1)}=1$, но порядок $x^{p-1}$ равен $p+1$.
Для любого $x^p\in S$ $n(x)$ - квадратичный невычет в $F_p$ иначе $(x^{p+1})^{\frac{p-1}{2}}=1$ и порядок $x^{p-1}$ делит $\frac{p+1}{2}<p+1$

4. Рассмотрим множество $B=\{x+x^{-1}+2|x\in S\}$. В нем $\frac{\varphi(p+1)}{2}$ элементов.
$B\subset F_p$
В $B$ все элементы - квадратичные невычеты в $F_p$.
Иначе $y=x^{p-1}+x^{1-p}+2=(x^{\frac{p-1}{2}}+x^{\frac{1-p}{2}})^2$,$x\in F_{p^2}$. Так как квадратных корней из числа $y$ только 2, то $x^{\frac{p-1}{2}}+x^{\frac{1-p}{2}}\in F_p$
$x^{\frac{p-1}{2}}+x^{p\frac{p-1}{2}}\in F_p$ - сумма сопряженных. Вычтем.
$x^{\frac{1-p}{2}}-x^{p\frac{p-1}{2}}=x^{\frac{1-p}{2}}(1-x^{\frac{p^2-1}{2}})\in F_p$
Если $1-x^{\frac{p^2-1}{2}}=0$ то порядок $x^{p-1}$ делит $\frac{p+1}{2}$ - противоречит определению $S$.
$(1-x^{\frac{p^2-1}{2}})\in F_p$ Значит $x^{\frac{1-p}{2}}\in F_p$
Для всех $z\in F^*_p, z^{1-p}=1$ Значит $(x^{p-1})^{\frac{p-1}{2}}=1$ - порядок $x^{p-1}$ делит $\frac{p-1}{2}$ - противоречит определению $S$

5. Пусть $A$ - множество первообразных корней $F_p$. Они все квадратичные невычеты в $F_p$.
Если $|A|+|B|>\frac{p-1}{2}$, то множества $A$ и $B$ пересекаются, так как квадратичных невычетов $\frac{p-1}{2}$.
Тогда если их пересечение содержит $c$, то $x^2+cx+c$ - искомый.
Действительно пусть $b(z)=c$. Такой $z$ существует по построению $B$.
Порядок $z^{p-1}$ Равен $p+1$. n(z) и с - невычеты. Значит существует $k\in F_p$, такое что $c=k^2 n(z)=n(kz)$. $-k$ - тоже подходит.
Порядок $(kz)^{p-1}=z^{p-1}$ равен $p+1$. Порядок $(kz)^{p+1}=n(kz)=c$ равен $p-1$. Значит порядок $kz$ равен $p^2-1$
$b(kz)=b(z)=c$ Значит $s(kz)^2=b(kz)n(kz)=c^2$. Значит $s(kz)=\pm c$. Заменив знак $k$ знак $s(kz)$ поменяется. Значит можно подобрать $k$ такое что $s(kz)=-c$. Тогда $x=kz$ - корень $x^2-s(x)x+n(x)=0$