Преобразование Карунена-Лоэва применительно к распознованию

[simplex1]

Цитата:

1) Что бросилось в глаза неправильные углы. По идеи они должны быть на 45 градусов повернуты.

Вы имеете ввиду на изображении?

Цитата:

2) Вроде как вектора должны располагаться в столбцах, а вы читаете по строкам.

Хочу уточнить этот момемент.
Допуститм у нас есть такое изображение: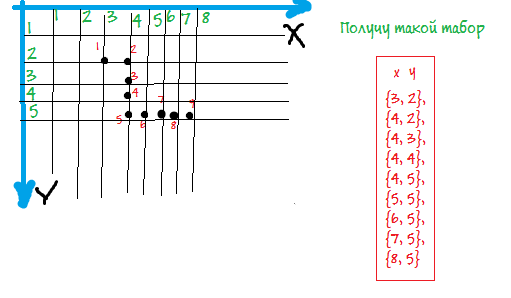

Данные формируются иммено так? Слобец пар из координат? При это не важнен порядок добавления этих точеку в столбец?
Я думал так, что если у меня столбец пар {x, y}. То и на выходе я получаю столбец из двух пар {x1,y1}, {x2, y2}. Которые определяют координаты главных компонент. Или не так?
Из такого столбца я получаю вот такие собственные числа и вектора, как мне их интерпритировать?

double[][] U = {
      {3, 2},
      {4, 2},
      {4, 3},
      {4, 4},
      {4, 5},
      {5, 5},
      {6, 5},
      {7, 5},
      {8, 5}
   };
   
   System.out.println("Origin matrix");
   Matrix m = new Matrix(U);
   m.print(5, 2);   
   
   System.out.println("Covariance matrix");
   Matrix cov = CovarianceMatrix.getCovarianceMatrix(m.getArray());
   cov.print(5, 2);
   
   EigenvalueDecomposition e = cov.eig();
   
   System.out.println("Eigen vectors");
   Matrix eigenVectors = e.getV();   
   eigenVectors.print(5, 2);

   System.out.println("Eigen values");
   Matrix eigenValues = e.getD();
   eigenValues.print(5, 2);

Origin matrix

3.00 2.00
4.00 2.00
4.00 3.00
4.00 4.00
4.00 5.00
5.00 5.00
6.00 5.00
7.00 5.00
8.00 5.00

Covariance matrix

2.75 1.50
1.50 1.75

Eigen vectors

0.58 0.81
-0.81 0.58

Eigen values

0.67 0.00
0.00 3.83


Где здесь координаты первой главной компоненты, а где второй?

Цитата:

3) Задайте длину векторов как собственные числа матрицы. И сверху ещё эллипс лучше построить для наглядности.

Это для визуализации только нужно, так? Или от этого зависит куда будут вектора направлены?

Цитата:

4) Перескок углов это неустойчивость. Нормально это или нет надо разбираться. Надо смотреть что у вас с ковариационной матрицей и что с собственными числами. Вектора обычно сортируют по собственным числам. А числа по величине.

Тестировал работу на примере вот от сюда:http://neuron-ai.tuke.sk/hudecm/science/9/9.html
На матрице, что у них, получаю:

Origin matrix

2.00 4.00 5.00 5.00 3.00 2.00
2.00 3.00 4.00 5.00 4.00 3.00

Covariance matrix

0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.50 0.50 0.00 -0.50 -0.50
0.00 0.50 0.50 0.00 -0.50 -0.50
0.00 0.00 0.00 0.00 0.00 0.00
0.00 -0.50 -0.50 0.00 0.50 0.50
0.00 -0.50 -0.50 0.00 0.50 0.50

Eigen vectors

-0.00 0.00 0.00 0.00 1.00 0.00
-0.29 0.79 -0.21 0.00 0.00 -0.50
-0.29 -0.21 0.79 0.00 0.00 -0.50
-0.00 0.00 0.00 1.00 0.00 0.00
0.29 0.58 0.58 0.00 0.00 0.50
-0.87 0.00 0.00 0.00 0.00 0.50

Eigen values

-0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 2.00


Если ее транспонировать, практически то что у них(только собственные вектора отличаются):

Origin matrix

2.00 2.00
4.00 3.00
5.00 4.00
5.00 5.00
3.00 4.00
2.00 3.00

Covariance matrix

1.90 1.10
1.10 1.10

Eigen vectors

0.57 0.82
-0.82 0.57

Eigen values

0.33 0.00
0.00 2.67


Почем так разняться результаты?

Цитата:

5) Как я уже писал от жеста зависит результат. В одних случаях собственные числа будут близкими в других нет. Если числа близкие то чехорда с векторами может наблюдаться из-за случайных помех.

Понял. Нужно брать хорошо различимые жесты.

З.Ы. Скажите пожалуйста. Если использовать эвклидово расстояние, то примерный алгоритм такой:
1. в базе будут храниться изображения жестов(различной ориентации: сверху, слева, справа, снизу)
2. с каждым из изображений я делаю то же что раньше.
2.1 Предвариетельная обработка(фильтрация, выделение руки)
2.2 Канни
2.3 Получаю собственные вектора и значения.
3. На вход подается неизвестное изображение.
4. Для него выполняются шаги 2.1-2.3
Вопрос: между чем ищется эвклидово расстояние(между значения?). То индус, код которого я пытаюсь понять. Предварительно изображения из базы еще и уменьшал до размеров 20х20. Это оправдано?
Могу ли я добавить пунск 2.4 - "уменьшение размеров"

З.Ы.Ы Спасибо большое что помогаете. Без Вас мне был бы каюк.

[Pavia]

simplex1
Нельзя применять инструмент, если не понимаешь как он работает. Ошибки из-за того что вы решили проскочить. Для этого надо вернуться назад и пройтись подробно по задачи расписав все шаги подробно. С расписыванием всех свойств и теорем.
Для этого вам надо прочитать про собственные вектора и собственные значения. И про то, как их вычисляют.
Думаю ответы вы сможете найти в книгах:
Р. Хорн , Джонсон.-Матричный анализ(1989)
Под общ. ред. Апатенок Р. Ф.-Элементы линейной алгебры.-Вышэйшая школа(1977)
Уилкинсон Дж., Райнш Ц.-Справочник алгоритмов на языке АЛГОЛ. Линейная алгебра(1976)
А.Н. Канатников, А.П. Крищенко - Линейная алгебра.Математика в техническом университете том IV. Изд-во МГТУ им. Н.Э. Баумана (2002)

А также вам надо прочитать справку по функциям которые вы используете.

[simplex1]

Ой мама. Как же я задолбался. Помогите еще раз, прошу. Делаю так:
Пытаюсь реализовать разпование, используя эвклидово расстояние.
1. Эпат обучение
1.1 Зарание приготовил по 80 изображение жестов(только контуры - после Канни) для 5 жестов.
Тапа такого:


1.2. Получается 5 * 80 = 400 - это высота матрицы(количество строк). Размер изображение 150х150, масштабирую до 20х20 = 40 - это ширина матрицы(количество столбцов).
Получается примерно такок:


Все эти картинки читаю в матрицу(dataset) 400х40. Каждая строка - это массив пикселей. Значение массива - значение RGB.

private static double[] imageToVector(BufferedImage image) {
   int h = image.getHeight();
   int w = image.getWidth();
   int[] pixels = image.getRGB(0, 0, w, h, null, 0, w);
   double[] vector = new double[pixels.length];
   for (int k = 0; k < pixels.length; ++k)
       vector[k] = pixels[k];

   return vector;
    }

private static double[][] buildDataset(String[] fileList) {
   double[][] dataset = new double[fileList.length][];
   for (int i = 0; i < fileList.length; i++)
       dataset[i] = imageToVector(loadImage(fileList[i], sDatabasePath));

   return dataset;
    }

1.3. Далее нахожу в каждом столбце среднее. Вычитаю это значение из всех элементов столбца.

 private static double[] centering(double[][] dataset) {
   int h = dataset.length;//height
   int w = dataset[0].length;//width
   double average[] = new double[w];
   for (int x = 0; x < w; ++x) {
       for (int y = 0; y < h; ++y) {
      average[x] += dataset[y][x];
       }
       average[x] /= h;
   }
   for (int y = 0; y < h; y++) {
       for (int x = 0; x < w; x++) {
      dataset[y][x] -= average[x];
       }
   }

   return average;
    }

1.4. Далее нахожу ковариоционную матрицу(Код из библиотеки - ошибок нет):

Matrix gestures = new Matrix(mDataset, mHeight, mWidth);
Matrix cv = gestures.times(gestures.transpose());// Covariance  matrix

*times - перемноежение матриц
1.5. Далее нахожу собственные значения и вектора. Последние сортирую

EigenvalueDecomposition e = cv.eig();
   double[] eigValues = readDiagonal(e.getD().getArray());
   mEigenvectors = e.getV().getArray();
   int[] index = new int[mHeight];
   double[][] tempVector = new double[mHeight][mWidth];
   for (int i = 0; i < mHeight; i++) {
       index[i] = i;
   }
   doubleQuickSort(eigValues, index, 0, mHeight - 1);
   int[] tempIndex = new int[mHeight];
   for (int j = 0; j < mHeight; j++) {
       tempIndex[mHeight - 1 - j] = index[j];
   }
   index = tempIndex;
   for (int col = mHeight - 1; col >= 0; col--) {
       for (int rows = 0; rows < mHeight; rows++) {
      tempVector[rows][col] = mEigenvectors[rows][index[col]];
       }
   }
   mEigenvectors = tempVector;

1.6. Далее перемножаю собственные вектора на исходную матрицу(gestures - она же datase)

Matrix ev = new Matrix(mEigenvectors, mHeight, mHeight);// Eigen vectors
mEigenvectors = ev.times(gestures).getArray();   

1.7 Нормализую вектора

/* Normalize our eigenvector matrix. */
   for (int y = 0; y < mHeight; y++) {
       double max = findMax(mEigenvectors[y]); // Our max
       for (int x = 0; x < mEigenvectors[0].length; x++)
      mEigenvectors[y][x] = Math.abs(mEigenvectors[y][x] / max);// Normalize
   }

1.8. Вычисляю порогую матрицу(вроде так называется. еще пишут wk - но не знаю как это расшифровуется)

private static void computeThreshold() {
   mThresholds = new double[mHeight][sQuantityVectors];
   for (int i = 0; i < mHeight; i++) {
       for (int j = 0; j < sQuantityVectors; j++) {
      double sum = 0.0d;
      for (int k = 0; k < mWidth; k++) {
          sum += mEigenvectors[j][k] * mGestures[i][k];
      }
      mThresholds[i][j] = Math.abs(sum);
       }
   }
    }

*sQuantityVectors количество векторов, которые мы будут использовать. Которые несут максим информации(по нашему мнению)

На этом обучение закончено
2. Этап распознование
На вход подается изображение(Канни, потом масштабирование - 20х20)

public static void recognize(BufferedImage unrecognized) {
   double[] inputImage = imageToVector(unrecognized);
   for (int pixel = 0; pixel < inputImage.length; pixel++) {
       inputImage[pixel] = inputImage[pixel] - mAverage[pixel];
   }
   double[] input = new double[sQuantityVectors];
   for (int image = 0; image < sQuantityVectors; image++) {
       double sum = 0.0d;
       for (int pixel = 0; pixel < mWidth; pixel++)
      sum += mEigenvectors[image][pixel] * inputImage[pixel];
       input[image] = Math.abs(sum);
       sum = 0;
   }
   /*
    * Find the minimun distance from the input_wk as compared to wk
    */
   int index = 0;
   double[] distance = new double[sQuantityVectors];
   double[] minDistance = new double[sQuantityVectors];

   for (int y = 0; y < mHeight; y++) {
       for (int j = 0; j < sQuantityVectors; j++)
      distance[j] = Math.abs(input[j] - mThresholds[y][j]);
       if (y == 0)
      System.arraycopy(distance, 0, minDistance, 0, sQuantityVectors);
       if (sum(minDistance) > sum(distance)) {
      index = y;
      System.arraycopy(distance, 0, minDistance, 0, sQuantityVectors);
       }
   }
   String mathName = mFileList[index]
           .substring(0, mFileList[index].indexOf("."))
           .replaceAll("\\d", "").toLowerCase().trim();
   sMatchingImage = mathName;
    }

Что я делаю не так? Помогите, умоляю. У меня уже просто нет идей.

Спасибо!

[simplex1]

Я никак не могу понять, можно ли формировать исходный вектор из значений яркости пикселей?
Вы писали, что нужно создавать вектор пар {x, y}. Но ведь длина котура может быть разной - отсда разный размер вектора. Как тогда их обрабатывать?

[Pavia]

simplex1
Не понял, что за алгоритм выше?
1.2 Зачем-то объединяются одинаковые жесты. Порог как-то странно вычисляются.
Во-вторых изображения не отцентрированы. Прекрасно видно на 4 жесте.
Я бы распознавание просто сделал по шаблонам. У вас есть 80 образцов каждого жеста. Когда вы вычислили углы собственного вектора вы знаете как повернуть изображение так чтобы углы не влияли. Но разброс по углам большой, поэтому до конца это не решает проблему.
Поэтому и нужно несколько шаблонов. Масштабируем шаблоны до $20х20$ И собственно проверяем насколько каждый эталон похож на шаблон.
Вычитаем и считаем Евклидову метрику. Далее ищем минимальное расстояние по этой метрике между эталоном и шаблоном. Это наше изображение.
Потребуется перебрать всего $20*20*80*5$

Можно внутри группы усреднить изображения. Что сократит перебор до $20*20*5$
Но качество распознавания пострадает.

Что-бы повысить распознавании надо вначале выделить наиболее назначаемые пиксели.
Наиболее отличные между разными жестами. А остальное занулить.
Т.е. такие у которых наибольшие сингулярные числа те и наиболее значимы.

Переводим наши эталоны в форму $400*5$
Ищем сингулярные числа и сингулярные вектора их у нас должно получиться по 400.
Далее наименьшие числа зануляем и собираем матрицу обратно.
Всё теперь у нас 5 эталонов 20х20 с которыми мы можем сравнивать наш шаблон по евклидовой метрике.


Разная длина контура будет. У ковариационной матрицы будут разные собственные числа. Но поворот и собственные вектора от этого не зависят.
Да и во вторых вы же масштабируете изображения.

[simplex1]

Цитата:

Не понял, что за алгоритм выше?

Вот http://progcoders.wordpress.com/2013/03/02/face-recognition-using-kl-transforms/
Там какой-то индус написал программу для распознования лиц. Я разобрался в коде и прикрутил его себе. Если мою версию применить для распознования лиц, как у него. То работатет все нормально. Но когда речь идет о динамических жестах, то все валится. Результаты отвратительные. Отличить получается только жесты влево, вправо и ок. Все отстально практически не распознается.

Цитата:

Во-вторых изображения не отцентрированы. Прекрасно видно на 4 жесте.

Понял. Исправлю.

Я уже перестаю что-либо понимать. Беда бедой. Пойду на пересдачу 100%. Цельный месяц бьюсь с этим преобразованием. С места не сдвинулся. Каша в голове полнейшая.

Понимаю что я вас уже задолбал. Я не настолько силен в линейной алгебре как Вы.
Поясните пожалуйста этот момент, а то я немного запустался

Цитата:

Поэтому и нужно несколько шаблонов. Масштабируем шаблоны до $20х20$ И собственно проверяем насколько каждый эталон похож на шаблон.
Вычитаем и считаем Евклидову метрику. Далее ищем минимальное расстояние по этой метрике между эталоном и шаблоном. Это наше изображение.
Потребуется перебрать всего...

Что есть шаблон, а что эталон?

Цитата:

Вычитаем и считаем Евклидову метрику

Вот с этим тоже проблема. Она считается межу собственными числами?

Не могу представить последовательность действий. Что за чем делается.

Я еще путаюсь вот из-за чего:
Мы работает с пикселя контура объекта или с всем изображением?

Спасибо, что помогаете.

[Pavia]

simplex1

simplex1 в сообщении #940987 писал(а):

Не могу представить последовательность действий. Что за чем делается.
Я еще путаюсь вот из-за чего:
Мы работает с пикселя контура объекта или с всем изображением?

И то и то.
Вначале используем контур что-бы избавится от зависимости от вращения.
А затем пиксели изображения из которых выбираем наиболее значимые.

simplex1 в сообщении #940987 писал(а):

Что есть шаблон, а что эталон?

Это я напутал. В предыдущем сообщение слово "шаблон" следует читать как "образец".
Эталон это образец с известным классом.
С эталоном сравнивается неизвестный образец.
Если они совпадают, то мы нашли к какому классу относится неизвестный образец.