Вероятно эта не та теорема Ферма о которой вы подумали. Простите меня за этот маркетинг).
Собственно тут речь о упражнении из Куранта, Роббинса "Что такое математика".
Скажите верно ли доказательство?
Теорема Ферма выглядит так:
Если  - простое число, не делящее целого числа
- простое число, не делящее целого числа  , то
, то
Ее доказывать не нужно, а предлагается доказать общую теорему Фурма (исходя из того, что вышеописанное уже доказано):
наименьшее число  , для которого
, для которого  , должно быть делителем
, должно быть делителем  .
.Можно записать, что

, (1)
где

Нужно доказать, что

, что и будет значить, что

- делитель

.
Так же по условию:

(2)

(3)
Подставим (1) в (2):


(4)
Рассмотрим

:
- Если

, то

- Если
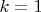
, то

, из условия (3)
- Если

, то

, опять же из условия (3) и свойства произведения сравнений
Из того, что во всех случаях

и из равенства (4), следует, что

Так как

- наименьшее число, для которого

, и

, то

только в случае

.
Что и требовалось доказать.
Меня смущает момент, что е - наименьшее число просто по условию. Не нужно ли это доказывать? Или я туплю?)