Добрый день!
Возник вопрос, какие уравнения относятся к гиперболическому типу среди уравнений

, где

, по повторяющимся индексам предполагается суммирование.
Я раньше думал, что такого вида уравнения называют гиперболическими, если существует 2 векторных поля
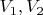
, таких что уравнение можно переписать в виде

, а характеристики - просто интегральные кривые этих векторных полей, но на примере уравнения

при

у меня найти таких двух полей не получилось, а оно гиперболическое, то есть, видимо, с такой трактовкой определения есть проблема. Вы не подскажете, в чём она конкретно заключается? Как её нужно подправить?