Подозреваю, что сначала нужно подтянуть знание общей физики.
Нафиг.
Для начала - вот:
Каждый узел сети здесь - математическая модель. В начале - одна простая. Потом каждая стрелочка означает усложнение модели определённого типа. Комбинацией всех таких усложнений получаются все остальные узлы.
Вам надо освоить математические модели и стрелочки, ведущие к узлу "
квантовая теория поля" (КТП), потому что эта теория и является математической моделью ФЭЧ. Делать это можно в любом порядке, только не "задом наперёд". Для общей эрудиции полезно знать и остальные незадействованные узлы и стрелочки, но для конкретной узкой цели - не обязательно. Итого, необходимо изучить:
I. Теоретическую механику (
механики Лагранжа и
Гамильтона).
II. Теорию поля (включая
специальную теорию относительности).
II. Квантовую механику.
III. Квантовую теорию поля.
Математические модели в них, соответственно:
- в теоретической механике -
система обыкновенных дифференциальных уравнений (в механике Лагранжа
2-го порядка, и в механике Гамильтона -
1-го порядка);
- в теории поля -
дифференциальные уравнения в частных производных. Кроме того, пространство независимых переменных ("пространство-время" на физическом языке) имеет
псевдоевклидову геометрию _
сигнатуры 
поэтому ДУЧП имеют соответствующую симметрию, и относятся к
гиперболическому типу.
- в квантовой механике - тоже ДУЧП, плюс алгебра
операторов на
функциональном пространстве. ДУЧП рассматривается как дифференциальное уравнение над оператором, решение которого -
оператор эволюции за конечное время.
- в квантовой теории поля - аналогичная алгебра операторов на несколько более сложном пространстве.
Но познакомиться с конкретными моделями мало. Надо набрать "словарный запас" конкретных физических задач, явлений, слов, которые в физике часто отличаются от математики.
Кроме того, (
IV) надо познакомиться, возможно бегло, с "зоопарком" известных частиц и теорий взаимодействий.
Я бы предложил:
I.
ЛЛ-1.
II(1).
ЛЛ-2 главы 1-4 + очень бегло главы 5-8. Обязательно § 52, повторить его перед III. Вспомнить методы решения ДУЧП 2 порядка.
II(2).
ЛЛ-3 главы 1-9 + потом главы 17-18.
Мессиа главы 3, 12, 21 (на будущее и по любопытствую - все остальные).
III. Это сложный вопрос, тут надо много учебников, и я плаваю. В любом случае, на эту часть надо оставить не меньше половины всего запланированного времени.
IV. Начать знакомство можно с
Окуня "Физика элементарных частиц",
Хелзена-Мартина,
Любимова-Киша. Их можно читать до III, а в разделе III - взять учебники, дающие кроме КТП конкретные теории взаимодействий.
-- 02.10.2014 01:12:16 --Добавлю картинку, которую нарисовал не я, а
Homo Sapiens (на некоторых форумах
homo unsapiens). Она показывает подход к ФЭЧ меньше со стороны теории, и больше со стороны практики:
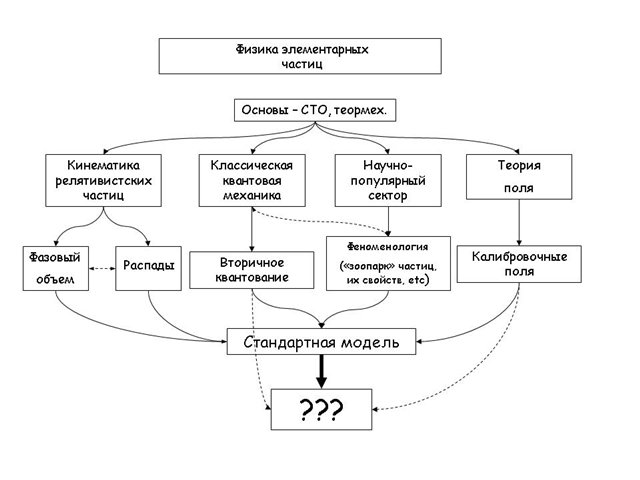
Здесь по кинематике пригодится
Копылов (для начала) и
Бюклинг-Каянти, а остальные клетки будут уже охвачены.



