Перенести всё в одну сторону,
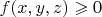
.
Найти минимум функции.
Показать что минимум

.
(Оффтоп)
В 50-60 годах неравнодушные граждане (не математики) любили доказывать большую теорему Ферма.
Матфаки ВУЗов были временами завалены доказательствами, причем по российско-советской традиции на доказательствах иногда стояла виза какого-нить горсовета "рассмотреть".
К главному, на одну из кафедр мехмата в те благословенные времена приходит телеграмма: "Доказал теорему Фема, основная идея - перенос

в левую часть. Подробности письмом"